- Paradoxe du coin
-
Paradoxe du coin
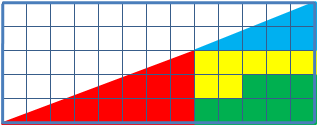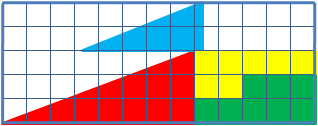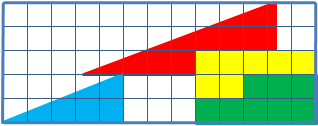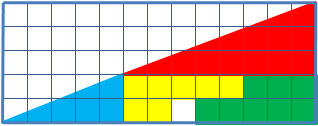Le paradoxe du coin en animation
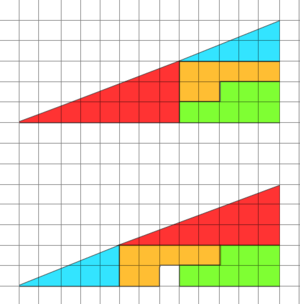
Le paradoxe du coin est une illusion d'optique. Si on découpe un triangle selon un quadrillage, de telle sorte que plusieurs constructions soient possibles, alors il y a certaines constructions où il manque un carré unitaire. C'est en effet très étonnant, car l'aire du triangle peut être décomposée : c'est la somme des carrés qui le composent - par extension la somme des carrés qui composent les formes de base. Dans notre exemple :
- Vert : 8 carrés
- Orange : 7 carrés
- Bleu : 5 carrés
- Rouge : 12 carrés
Cela donne un triangle d'aire 12 + 5 + 7 + 8 = 32. Or si on applique la formule de l'aire au triangle, on obtient 13 × 5 / 2 = 32,5. Le triangle manquant dans certaines formations correspond à cette « demi-unité » d'aire manquante, qui apparaît donc une fois sur deux !
Bien entendu, ce paradoxe s'explique très simplement. Il suffit de constater que la figure présentée comme un triangle n'en est pas un : l'« hypoténuse » est légèrement concave ou convexe, selon le cas. On peut pour s'en convaincre comparer les angles des deux « triangles », environ 22° ou 23,6° pour l'angle aigu, et 66,4° ou 68° pour l'autre, selon la figure choisie. Ainsi la somme des trois angles est dans un cas inférieure et dans l'autre cas supérieure à 180°.
Finalement, la « surface manquante » ne fait que compenser l'écart entre la légère convexité et la légère concavité des prétendus triangles.
Cette construction géométrique est liée à la suite de Fibonacci. En effet, la différence entre le produit de deux termes consécutifs de cette suite (ici 3 et 5) et le produit des deux termes adjacents (ici 2 et 8) vaut toujours 1. On peut donc réaliser sur le même principe de faux triangles de côtés 2 et 5, 3 et 8, 5 et 13 (comme ici), 8 et 21, etc.
Il existe d'autres illusions d'optique du même type reposant toujours sur une astuce difficilement perceptible par un spectateur non averti.
Liens externes
Portail des mathématiques
Catégories : Paradoxe en mathématiques | Illusion d'optique
Wikimedia Foundation. 2010.
