Paradoxe de Borel-Kolmogorov

Paradoxe de Borel-Kolmogorov

Paradoxe de Borel

Le paradoxe de Borel (parfois appelé le paradoxe de Borel-Kolmogorov) est un paradoxe de la théorie des probabilités en rapport avec les probabilités conditionnelles et les densités de probabilité.

Supposons que nous ayons deux variables aléatoires, X et Y, de densité de probabilité conjointe pX,Y(x,y). Nous pouvons former la densité conditionnelle de Y sachant X,

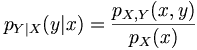
p_{Y|X}(y|x) = \frac{p_{X,Y}(x,y)}{p_{X}(x)}

où pX(x) est la loi marginale appropriée.

En utilisant le théorème du changement de variable, nous pouvons paramétrer la loi conjointe avec les fonctions U= f(X,Y), V = g(X,Y), et pouvons alors former la densité conditionnelle de V sachant U.

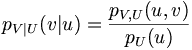
p_{V|U}(v|u) = \frac{p_{V,U}(u,v)}{p_{U}(u)}

Étant donné une condition particulière sur X et la condition équivalente sur U, l’intuition nous suggère que les densités conditionnelles pY|X(y|x) and pV|U(v|u) devraient être identiques. Ce n’est pas le cas en général.

Sommaire

Un exemple concret

Une loi uniforme

Soit la densité de probabilité conjointe

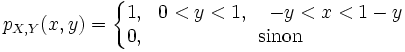
p_{X,Y}(x,y) =\left\{\begin{matrix} 1, & 0 < y < 1, \quad -y < x < 1 - y \\ 0, & \mbox{sinon} \end{matrix}\right.

La densité marginale de X se calcule

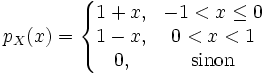
p_X(x) =\left\{\begin{matrix} 1+x, & -1 < x \le 0 \\ 1 - x, & 0 < x < 1 \\ 0, & \mbox{sinon}\end{matrix}\right.

Ainsi la densité conditionnelle de Y sachant X est

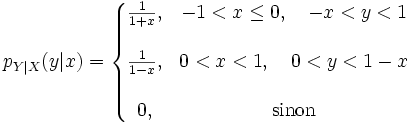
p_{Y|X}(y|x) =\left\{\begin{matrix} \frac{1}{1+x}, & -1 < x \le 0, \quad -x < y < 1 \\ \\ \frac{1}{1-x}, & 0 < x < 1, \quad 0 < y < 1 - x \\ \\ 0, & \mbox{sinon}\end{matrix}\right.

qui est uniforme suivant y.

Nouveau paramétrage

Maintenant, appliquons la transformation suivante :

U = \frac{X}{Y} + 1 \qquad \qquad V = Y.

En utilisant le théorème du changement de variable, nous obtenons

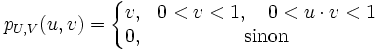
p_{U,V}(u,v) =\left\{\begin{matrix} v, & 0 < v < 1, \quad 0 < u \cdot v < 1 \\ 0, & \mbox{sinon} \end{matrix}\right.

La distribution marginale se calcule et est égale à

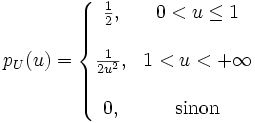
p_U(u) =\left\{\begin{matrix} \frac{1}{2}, & 0 < u \le 1 \\ \\ \frac {1}{2u^2}, & 1 < u < +\infty \\ \\ 0, & \mbox{sinon}\end{matrix}\right.

Ainsi la densité conditionnelle de V sachant U est

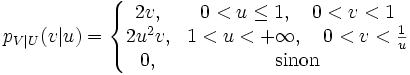
p_{V|U}(v|u) =\left\{\begin{matrix} 2v, & 0 < u \le 1, \quad 0 < v < 1 \\ 2u^2v, & 1 < u < +\infty, \quad 0 < v < \frac{1}{u} \\ 0, & \mbox{sinon}\end{matrix}\right.

qui n’est pas uniforme suivant v.

Le résultat non intuitif

D'après ce qui précède, nous avons

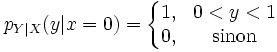
p_{Y|X}(y|x=0) = \left\{\begin{matrix} 1, & 0 < y < 1 \\ 0, & \mbox{sinon}\end{matrix}\right.

La condition équivalente dans le système de coordonnées u-v est U = 1, et la densité conditionnelle de V sachant U = 1 est

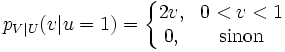
p_{V|U}(v|u=1) = \left\{\begin{matrix} 2v, & 0 < v < 1 \\ 0, & \mbox{sinon}\end{matrix}\right.

Paradoxalement, V = Y et X = 0 est identique à U = 1, mais

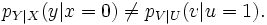
p_{Y|X}(y|x = 0) \ne p_{V|U}(v|u = 1).

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Paradoxe de Borel ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Paradoxe de Borel-Kolmogorov de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Paradoxe de borel — Le paradoxe de Borel (parfois appelé le paradoxe de Borel Kolmogorov) est un paradoxe de la théorie des probabilités en rapport avec les probabilités conditionnelles et les densités de probabilité. Supposons que nous ayons deux variables… …   Wikipédia en Français

  • Paradoxe de Borel — Le paradoxe de Borel (parfois appelé le paradoxe de Borel Kolmogorov) est un paradoxe de la théorie des probabilités en rapport avec les probabilités conditionnelles et les densités de probabilité. Supposons que nous ayons deux variables… …   Wikipédia en Français

  • Loi Du Zéro Un De Kolmogorov — En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Loi du zero un de Kolmogorov — Loi du zéro un de Kolmogorov En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la… …   Wikipédia en Français

  • Loi du zéro-un de Kolmogorov — En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Loi du zéro un de kolmogorov — En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Loi du zéro un de Kolmogorov — En probabilités, la loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Suite aléatoire — Cette suite est elle aléatoire ? En mathématiques, une suite aléatoire, ou suite infinie aléatoire, est une suite de nombres ne possédant aucune structure, régularité, ou règle de prédiction identifiable. Une telle suite correspond à la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”