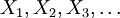Loi du zero un de Kolmogorov

Loi du zero un de Kolmogorov

Loi du zéro un de Kolmogorov

En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C'est-à-dire que la probablité d'un tel événement vaut 1 ou 0.

Les événements queues se définissent en termes de suites infinies de variables aléatoires. Soit

X_1,X_2,X_3,\dots\,

une suite[2] infinie de variables aléatoires indépendantes. Alors, un événement queue est un événement dont la réalisation est déterminée par la valeur des variables Xi, mais qui est indépendant de toute sous-suite finie de variables Xi.

  • Par exemple, l'événement "la série 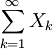\sum_{k=1}^\infty X_k converge" est un événement queue.
  • L'événement 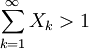\sum_{k=1}^\infty X_k > 1 n'est pas un événement queue puisque, par exemple, il n'est pas indépendant de la valeur de X1.
  • Pour une infinité de lancers d'une pièce à pile ou face, le fait qu'une séquence de 100 "faces" consécutives soit réalisée une infinité de fois, est un événement queue.
  • Le paradoxe du singe savant est un exemple d'application de la Loi zéro un.

De façon surprenante, il est parfois aisé de prouver grâce à cette loi qu'un événement a une probabilité dans {0,1}, mais très difficile de déterminer laquelle de ces deux valeurs est la bonne.

Démonstration

L'indépendance des Xk conduit à celle des tribus Un = σ(Xk;k < n) et Tn = σ(Xk;k > = n)

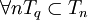
Si nous notons Tq la tribu de queue, on a \forall n T_q \subset T_n

Ce qui nous assure, pour tout n, l'indépendance de Tq et Un.

Posons alors Uq la tribu engendrée par les Un pour tout n.

La suite de tribus 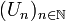(U_n)_{n \in \mathbb{N}} est croissante, donc sa limite 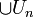\cup U_n est un π-système qui engendre Uq. Comme 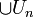\cup U_n et Tq sont indépendants, Uq et Tq le sont.

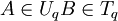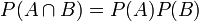Ainsi pour tout événements A \in U_q B \in T_q on a P(A \cap B) = P(A)P(B).

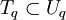Or comme T_q \subset U_q , on prend A=B ce qui donne P(A) = P(A)2

On en conclut que P(A)=0 ou 1

Notes

  1. ↑ "tail events" en anglais.
  2. ↑ les variables Xi n'ont pas forcément la même distribution de probabilité.

Voir aussi

  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Loi du z%C3%A9ro un de Kolmogorov ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi du zero un de Kolmogorov de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Loi Du Zéro Un De Kolmogorov — En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Loi du zéro-un de Kolmogorov — En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Loi du zéro un de kolmogorov — En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Loi du zéro un de Kolmogorov — En probabilités, la loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un tel événement …   Wikipédia en Français

  • Loi du zéro-un — de Kolmogorov En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un …   Wikipédia en Français

  • Loi du zéro un — de Kolmogorov En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la probablité d un …   Wikipédia en Français

  • Loi du zéro-un de Borel — La loi du zéro un de Borel a été publiée en 1909 dans l article Les probabilités dénombrables et leurs applications arithmétiques[1], par Émile Borel, en vue de la démonstration du théorème des nombres normaux, et en vue d applications aux… …   Wikipédia en Français

  • Loi du 0-1 — Loi du zéro un de Kolmogorov En probabilités, la Loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues[1], soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. C est à dire que la… …   Wikipédia en Français

  • Kolmogorov — Andreï Kolmogorov Andreï Kolmogorov Andreï Nikolaïevitch Kolmogorov (en russe : Андрей Николаевич Колмогоров ; 25 avril 1903 à Tambov 20 octobre 1987 à …   Wikipédia en Français

  • Loi forte des grands nombres — Une loi forte des grands nombres est une loi mathématique selon laquelle la moyenne des n premiers termes d une suite de variables aléatoires converge presque sûrement vers une constante (non aléatoire), lorsque n tend vers l infini. Lorsque ces… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”