Paradoxe d'achille et de la tortue

Dans le paradoxe d'Achille et de la tortue, formulé par Zénon d'Élée, il est dit qu'un jour, le héros grec Achille a disputé une course à pied avec le lent reptile. Comme Achille était réputé être un coureur très rapide, il avait accordé gracieusement à la tortue une avance de cent mètres.

Zénon d'Élée affirme alors que le rapide Achille n'a jamais pu rattraper la tortue. « En effet, supposons pour simplifier le raisonnement que chaque concurrent court à vitesse constante, l'un très rapidement, et l'autre très lentement ; au bout d'un certain temps, Achille aura comblé ses cent mètres de retard et atteint le point de départ de la tortue ; mais pendant ce temps, la tortue aura parcouru une certaine distance, certes beaucoup plus courte, mais non nulle, disons un mètre. Cela demandera alors à Achille un temps supplémentaire pour parcourir cette distance, pendant lequel la tortue avancera encore plus loin ; et puis une autre durée avant d'atteindre ce troisième point, alors que la tortue aura encore progressé. Ainsi, toutes les fois qu'Achille atteint l'endroit où la tortue se trouvait, elle se retrouve encore plus loin. Par conséquent, le rapide Achille n'a jamais pu et ne pourra jamais rattraper la tortue ».

Résolution

En analyse moderne, le paradoxe est résolu en utilisant fondamentalement le fait qu'une série infinie de nombres strictement positifs peut converger vers un résultat fini.

En l'occurrence, ce paradoxe fonctionne en découpant un événement d'une durée finie (Achille rattrape la tortue) en une infinité d'événements de plus en plus brefs (par exemple, Achille fait 99% de la distance manquante). Ensuite, l'erreur mathématique introduite dans le paradoxe consiste à affirmer que la somme de cette infinité d'événements de plus en plus brefs tend vers l'infini, c'est-à-dire qu'Achille n'arrive jamais (temps infini) à rattraper la tortue.

Numériquement, admettons que chaque étape est 100 fois plus brève que la précédente. Si l'on considère que la première étape a pris 10 secondes, alors la suivante a pris 0,1 seconde et on obtient la série suivante : T = 10 + 0,1 + 0,001 + 0,00001… = 10,10101… secondes. Ce paradoxe montre donc simplement qu'Achille ne peut pas rejoindre la tortue en moins de 10,10 secondes. Mathématiquement, on peut écrire la somme sous cette forme :

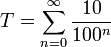
Il s'agit d'une série géométrique de raison ¹⁄₁₀₀ et de terme initial 10. Ceci nous assure de sa convergence :

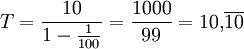
On notera aussi qu'à travers ce paradoxe, existe une volonté de montrer que l'infiniment petit n'existe pas. Pensée également partagée par Démocrite, l'inventeur de la notion d'atome. La physique quantique va elle aussi dans ce sens en admettant l'existence d'une unité de temps et d'une unité de taille toutes deux indivisibles (approximativement 10^-44 secondes et 10^-33 mètres). Cette hypothèse de non-nexistence de l'infiniment petit n'est cependant pas nécessaire à la solution analytique du problème. La série mathématique considérée converge, que l'on considère le temps comme discret ou continu.

Source

• La Physique VI:9, 239b15, Aristote

Voir aussi

• Paradoxes de Zénon
• Paradoxe de la flèche
• What the Tortoise Said to Achilles

• Portail de la philosophie antique
• Portail de la philosophie
• Portail de la Grèce antique
• Portail des mathématiques