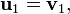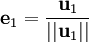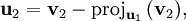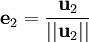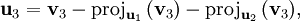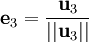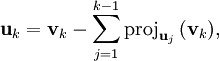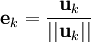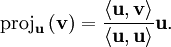Orthonormalisation de Schmidt
- Orthonormalisation de Schmidt
-
Procédé de Gram-Schmidt
En algèbre linéaire, dans un espace vectoriel muni d'un produit scalaire, le procédé de Gram-Schmidt[1], en notant ![N= [0,p]\,](/pictures/frwiki/50/2f6bce44984c0ebf193ada154043c3e6.png) ou
ou 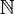 est un algorithme pour construire de proche en proche une base orthonormée à partir d'une base donnée.
est un algorithme pour construire de proche en proche une base orthonormée à partir d'une base donnée.
Précisément :
On oublie souvent la condition d'unicité. Elle permet de parler de l 'orthonormalisée de Gram-Schmidt.
L'étape générale de l'algorithme consiste à soustraire au vecteur vj + 1 sa projection orthogonale sur l'espace Fj. On s'appuie sur la famille orthonormale déjà construite pour le calcul de projection.
Cette méthode a été nommée en hommage à Jørgen Pedersen Gram et Erhard Schmidt, mais elle est plus ancienne et est retrouvée dans des travaux de Laplace et Cauchy.
Applications.
- Le procédé d'orthonormalisation de Gram-Schmidt donne (constructivement !) l'existence de bases orthonormées pour tout espace euclidien ou hermitien.
- On peut aussi orthonormaliser la base canonique (1,X,...)de R[X] et obtenir ainsi une famille de polynômes orthogonaux.
Procédé de Gram-Schmidt
Nous définissons l'opérateur de projection sur une droite vectorielle par :
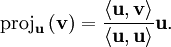
Le procédé de Gram-Schmidt est alors :
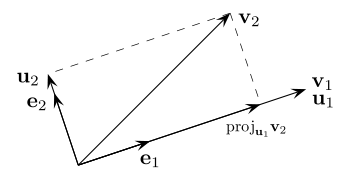
Les deux premières étapes du procédé de Gram–Schmidt.
Notes et références
- ↑ Mathématiques Tout-en-un . 2e année MP, Dunod, 2004, 2e éd. (ISBN 2-10-007576-4), p. 569
 Portail des mathématiques
Portail des mathématiques
Catégories : Algèbre bilinéaire | Algorithme
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Orthonormalisation de Schmidt de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Orthonormalisation de Gram-Schmidt — Procédé de Gram Schmidt En algèbre linéaire, dans un espace vectoriel muni d un produit scalaire, le procédé de Gram Schmidt[1], en notant ou est un algorithme pour construire de proche en proche une base orthonormée à partir d une base donnée.… … Wikipédia en Français
Procédé de Gram-Schmidt — En algèbre linéaire, dans un espace préhilbertien (c est à dire un espace vectoriel sur le corps des réels ou celui des complexes, muni d un produit scalaire), le procédé de Gram Schmidt[1] est un algorithme pour construire, à partir d une… … Wikipédia en Français
Gram-Schmidt — Procédé de Gram Schmidt En algèbre linéaire, dans un espace vectoriel muni d un produit scalaire, le procédé de Gram Schmidt[1], en notant ou est un algorithme pour construire de proche en proche une base orthonormée à partir d une base donnée.… … Wikipédia en Français
Lemme d'orthonormation de Gram-Schmidt — Procédé de Gram Schmidt En algèbre linéaire, dans un espace vectoriel muni d un produit scalaire, le procédé de Gram Schmidt[1], en notant ou est un algorithme pour construire de proche en proche une base orthonormée à partir d une base donnée.… … Wikipédia en Français
Procede de Gram-Schmidt — Procédé de Gram Schmidt En algèbre linéaire, dans un espace vectoriel muni d un produit scalaire, le procédé de Gram Schmidt[1], en notant ou est un algorithme pour construire de proche en proche une base orthonormée à partir d une base donnée.… … Wikipédia en Français
Procédé de gram-schmidt — En algèbre linéaire, dans un espace vectoriel muni d un produit scalaire, le procédé de Gram Schmidt[1], en notant ou est un algorithme pour construire de proche en proche une base orthonormée à partir d une base donnée. Précisément … Wikipédia en Français
Theoreme de Riesz — Théorème de Riesz En mathématiques, et plus particulièrement en théorie des espaces vectoriels normés réels ou complexes, le théorème de Riesz établit un lien entre la notion de compacité, une propriété topologique, et celle de dimension, une… … Wikipédia en Français
Théorème de riesz — En mathématiques, et plus particulièrement en théorie des espaces vectoriels normés réels ou complexes, le théorème de Riesz établit un lien entre la notion de compacité, une propriété topologique, et celle de dimension, une notion algébrique. Il … Wikipédia en Français
HILBERT (ESPACE DE) — La théorie des espaces hilbertiens trouve son origine dans celle des développements de fonctions arbitraires en séries de fonctions orthogonales, lesquelles apparaissent le plus souvent comme fonctions propres de certains opérateurs différentiels … Encyclopédie Universelle
Base Orthonormale — Pour les articles homonymes, voir BON. Une base orthonormale (BON) est une structure mathématique. Sommaire 1 Définition 2 Repère orthonormal (ou orthonormé) … Wikipédia en Français
![N= [0,p]\,](/pictures/frwiki/50/2f6bce44984c0ebf193ada154043c3e6.png) ou
ou 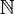 est un algorithme pour construire de proche en proche une base orthonormée à partir d'une base donnée.
est un algorithme pour construire de proche en proche une base orthonormée à partir d'une base donnée.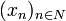 est une famille libre d'un espace préhilbertien, il existe une et une seule famille orthonormée
est une famille libre d'un espace préhilbertien, il existe une et une seule famille orthonormée 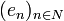 telle que :
telle que :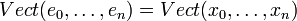 pour tout
pour tout 
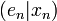 est strictement positif
est strictement positif