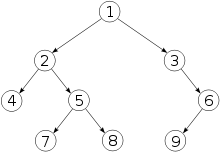
Arbre binaire

En informatique, un arbre binaire est une structure de données qui peut se représenter sous la forme d'une hiérarchie dont chaque élément est appelé nœud, le nœud initial étant appelé racine. Dans un arbre binaire, chaque élément possède au plus deux éléments fils au niveau inférieur, habituellement appelés gauche et droit. Du point de vue de ces éléments fils, l'élément dont ils sont issus au niveau supérieur est appelé père.

Au niveau le plus élevé il y a donc un nœud racine. Au niveau directement inférieur, il y a au plus deux nœuds fils. En continuant à descendre aux niveaux inférieurs, on peut en avoir quatre, puis huit, seize, etc. c'est-à-dire la suite des puissances de deux. Un nœud n'ayant aucun fils est appelé feuille. Le nombre de niveaux total, autrement dit la distance entre la feuille la plus éloignée et la racine, est appelé hauteur de l'arbre.

Le niveau d'un nœud est appelé profondeur.

Les arbres binaires peuvent notamment être utilisés en tant qu'arbre binaire de recherche ou en tant que tas binaire.

Sommaire 1 Définition selon le NIST 2 Définition dans la théorie des graphes 3 Types d'arbre binaire 4 Méthode pour stocker des arbres binaires 5 Méthode d'itération des arbres binaires 5.1 Parcours préfixe, infixe et postfixe 5.1.1 Parcours préfixe 5.1.2 Parcours postfixe 5.1.3 Parcours infixe 5.2 Ordre en profondeur 5.3 Parcours en largeur 6 Transformation d'un arbre quelconque en un arbre binaire 7 Voir aussi 7.1 Algorithmes utilisant des arbres binaires 7.2 Arbres binaires particuliers 7.3 Autres types d'arbres 8 Notes et références

Définition selon le NIST

Selon la définition rédigée par le National Institute of Standards and Technology (NIST), la hauteur d'un arbre qui a seulement un nœud, sa racine, vaut zéro^[1].

Définition dans la théorie des graphes

La théorie des graphes utilise la définition suivante : un arbre binaire est un graphe connexe acyclique, tel que le degré de chaque nœud (ou vertex) soit au plus 3.

La racine d'un arbre binaire est le nœud d'un graphe de degré maximum 2. Avec une racine ainsi choisie, chaque nœud aura un unique parent défini et deux fils ; toutefois, ces informations sont insuffisantes pour distinguer un fils droit d'un fils gauche. Si nous négligeons cette condition de connexité, et qu'il y a de multiples éléments connectés, on appellera cette structure une forêt.

Types d'arbre binaire

• Un arbre binaire (ou binaire-unaire) est un arbre avec racine dans lequel chaque nœud a au plus deux fils.

• Un arbre binaire entier est un arbre dont tous les nœuds possèdent zéro ou deux fils.

• Un arbre binaire parfait est un arbre binaire entier dans lequel toutes les feuilles (nœuds n'ayant aucun fils) sont à la même distance de la racine.

L'arbre binaire parfait est parfois nommé arbre binaire complet. Cependant certains définissent un arbre binaire complet comme étant un arbre binaire entier dans lequel les feuilles ont pour profondeur n ou n-1 pour un n donné.

Méthode pour stocker des arbres binaires

Les arbres binaires peuvent être construits à partir de primitives d'un langage de programmation de différentes manières. Dans un langage avec structures et pointeurs (ou références), les arbres binaires peuvent être conçus en ayant une structure à trois nœuds qui contiennent quelques données et pointeurs vers son fils droit et son fils gauche. L'ordre que cela impose aux nœuds enfants est parfois utile, en particulier pour les parcours infixes. Parfois, il contient également un pointeur vers son unique parent. Si un nœud possède moins de deux fils, l'un des deux pointeurs peut être affecté de la valeur spéciale nulle ; il peut également pointer vers un nœud sentinelle.

Les arbres binaires peuvent aussi être rangés dans des tableaux, et si l'arbre est un arbre binaire complet, cette méthode ne gaspille pas de place, et la donnée structurée résultante est appelée un tas. Dans cet arrangement compact, un nœud a un indice i, et (le tableau étant basé sur des zéros) ses fils se trouvent aux indices 2i+1 et 2i+2, tandis que son père se trouve (s'il existe) à l'indice floor((i-1)/2). Cette méthode permet de bénéficier d'un encombrement moindre, et d'un meilleur référençage, en particulier durant un parcours préfixe. Toutefois, elle requiert une mémoire contigüe, elle est coûteuse s'il s'agit d'étendre l'arbre et l'espace perdu (dans le cas d'un arbre binaire non complet) est proportionnel à 2^h - n pour un arbre de profondeur h avec n nœuds.

Dans les langages à union étiquetée comme ML, un nœud est souvent une union taguée de deux types de nœud, l'un étant un triplet contenant des données et ses fils droits et gauches, et l'autre un nœud vide, qui ne contient ni donnée ni fonction, ressemblant à la valeur nulle des langages avec pointeurs.

Méthode d'itération des arbres binaires

Souvent, il est souhaitable de visiter chacun des nœuds dans un arbre et d'y examiner la valeur. Il existe plusieurs ordres dans lesquels les nœuds peuvent être visités, et chacun a des propriétés utiles qui sont exploitées par les algorithmes basés sur les arbres binaires.

Parcours préfixe, infixe et postfixe

(parfois appelés préordre, inordre et postordre)

Soit une structure Arbre dont la racine est A et une référence gauche et droite à ses deux fils. Nous pouvons écrire les fonctions suivantes :

Parcours préfixe

VisiterPréfixe(Arbre A)
{
    Visiter(A)
    Si Non_Vide(gauche(A))
       VisiterPréfixe(gauche(A))
    Si Non_Vide(droite(A))
       VisiterPréfixe(droite(A))
}

Ceci affiche les valeurs de l'arbre en ordre préfixe. Dans cet ordre, chaque nœud est visité ainsi que chacun de ses fils.

Parcours postfixe

VisiterPostfixe(Arbre A) {
    Si Non_Vide(gauche(A))
       VisiterPostfixe(gauche(A))
    Si Non_Vide(droite(A))
       VisiterPostfixe(droite(A))
    Visiter(A)
}

Dans un parcours postfixe, on affiche chaque nœud après avoir affiché chacun de ses fils.

Parcours infixe

VisiterInfixe(Arbre A) {
    Si Non_Vide(gauche(A))
       VisiterInfixe(gauche(A))
    Visiter(A)
    Si Non_Vide(droite(A))
       VisiterInfixe(droite(A))
}

Un parcours infixe, comme ci-dessus, visite chaque nœud entre les nœuds de son sous-arbre de gauche et les nœuds de son sous-arbre de droite. C'est une manière assez commune de parcourir un arbre binaire de recherche, car il donne les valeurs dans l'ordre croissant.

Pour comprendre pourquoi cela est le cas, si n est un nœud dans un arbre binaire de recherche, alors tous les éléments dans le sous-arbre de gauche du nœud n seront inférieurs à n et ceux dans le sous-arbre de droite seront supérieurs ou égaux à n. Ainsi, si nous visitons le sous-arbre de gauche dans l'ordre, de manière récursive, puis que nous visitons n, et que nous visitons le sous-arbre de droite, nous aurons visité l'ensemble du sous-arbre enraciné en n dans l'ordre.

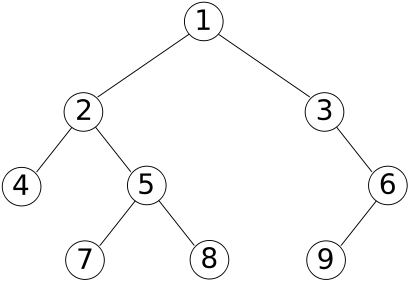
Dans cet arbre binaire, Rendu du parcours infixe : 4, 2, 7, 5, 8, 1, 3, 9, 6 Rendu du parcours postfixe : 4, 7, 8, 5, 2, 9, 6, 3, 1 Rendu du parcours préfixe : 1, 2, 4, 5, 7, 8, 3, 6, 9

Nous pouvons effectuer ces parcours avec un langage fonctionnel comme Haskell avec le code suivant :

data Tree a = Leaf | Node(a, Tree a, Tree a)

preorder Leaf = []
preorder (Node (x, left,right)) = [x] ++ (preorder left) ++ (preorder right)

postorder Leaf = []
postorder (Node (x, left,right)) = (postorder left) ++ (postorder right) ++ [x]

inorder Leaf = []
inorder (Node (x, left,right)) = (inorder left) ++ [x] ++ (inorder right)

Tous ces algorithmes récursifs utilisent une pile mémoire proportionnelle à la profondeur des arbres. Si nous rajoutons dans chaque nœud une référence à son parent, alors nous pouvons implémenter tous ces parcours en utilisant des espaces mémoires uniquement constants et un algorithme itératif. La référence au parent occupe cependant beaucoup d'espace ; elle n'est réellement utile que si elle est par ailleurs nécessitée ou si la pile mémoire est particulièrement limitée. Voici par exemple, l'algorithme itératif pour le parcours infixe :

VisiterInfixeIteratif(racine)
    precedent    := null
    actuel       := racine
    suivant      := null
   
    Tant que (actuel != null) Faire
        Si (precedent == pere(actuel)) Alors
            precedent := actuel
            suivant   := gauche(actuel)
        FinSi
        Si (suivant == null OU precedent == gauche(actuel)) Alors
            Visiter(actuel)
            precedent := actuel
            suivant   := droite(actuel)
        FinSi
        Si (suivant == null OU precedent == droite(actuel)) Alors
            precedent := actuel
            suivant   := pere(actuel)
        FinSi
        actuel := suivant
    FinTantQue

Ordre en profondeur

Avec ce parcours, nous tentons toujours de visiter le nœud le plus éloigné de la racine que nous pouvons, à la condition qu'il soit le fils d'un nœud que nous avons déjà visité. À l'opposé des parcours en profondeur sur les graphes, il n'est pas nécessaire de connaître les nœuds déjà visités, car un arbre ne contient pas de cycles. Les parcours préfixe, infixe et postfixe sont des cas particuliers de ce type de parcours.

Pour effectuer ce parcours, il est nécessaire de conserver une liste des éléments en attente de traitement. Dans le cas du parcours en profondeur, il faut que cette liste ait une structure de pile (de type LIFO, Last In, First Out autrement dit: « dernier entré, premier sorti »). Dans cette implémentation, on choisira également d'ajouter les fils d'un nœud de droite à gauche.

ParcoursProfondeur(Arbre A) {
   S = Pilevide
   ajouter(Racine(A), S)
   Tant que (S != Pilevide) {
       nœud = premier(S)
       retirer(S)
       Visiter(nœud) //On choisit de faire une opération
       Si (gauche(nœud) != null) Alors
           ajouter(gauche(nœud), S)
       Si (droite(nœud) != null) Alors
           ajouter(droite(nœud), S)
   }
}

Parcours en largeur

Contrairement au précédent, ce parcours essaie toujours de visiter le nœud le plus proche de la racine qui n'a pas déjà été visité. En suivant ce parcours, on va d'abord visiter la racine, puis les nœuds à la profondeur 1, puis 2, etc. D'où le nom parcours en largeur.

L'implémentation est quasiment identique à celle du parcours en profondeur à ce détail près qu'on doit cette fois utiliser une structure de file d'attente (de type FIFO, First in, first out autrement dit « premier entré, premier sorti »), ce qui induit que l'ordre de sortie n'est pas le même (i.e. on permute gauche et droite dans notre traitement).

ParcoursLargeur(Arbre A) {
   f = FileVide
   enfiler(Racine(A), f)
   Tant que (f != FileVide) {
       nœud = defiler(f)
       Visiter(nœud)                        //On choisit de faire une opération
       Si (gauche(nœud) != null) Alors
           enfiler(gauche(nœud), f)
       Si (droite(nœud) != null) Alors
           enfiler(droite(nœud), f)
   }
}

Transformation d'un arbre quelconque en un arbre binaire

Il existe une injection entre les arbres triés généraux et les arbres binaires, qui est spécialement utilisée par Lisp pour représenter les arbres triés généraux en tant qu'arbres binaires. Chaque nœud N dans l'arbre trié correspond au nœud N' dans l'arbre binaire ; le fils gauche de N' est le nœud correspondant au premier fils de N, et le fils droit de N' est le nœud correspondant au prochain frère de N - qui est le nœud suivant dans l'ordre parmi les enfants du père de N.

Une manière de se représenter ceci est de penser que chaque fils d'un nœud est dans une liste liée, mutuellement liés par leurs champs droits, et que le nœud possède seulement un pointeur vers le début de la liste, jusqu'à son champ gauche.

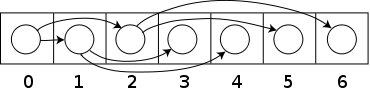
Par exemple, dans l'arbre de gauche, A a 6 fils : {B, C, D, E, F, G}. Il peut être converti en arbre binaire (comme celui de droite).

Cet arbre binaire peut être considéré comme l'arbre original incliné en longueur, avec les côtés noirs de gauche représentant les premiers fils et les côtés bleus de droite représentant ses prochains frères. La part de l'arbre de gauche pourrait être codée en Lisp comme ceci :

(((M N) H I) C D ((O) (P)) F (L))

qui pourrait être implémentée en mémoire comme l'arbre binaire de droite, sans les lettres de ce nœud qui ont un fils gauche.

Voir aussi

Algorithmes utilisant des arbres binaires

• Codage de Huffman
• Algorithme des nœuds chapeaux

Arbres binaires particuliers

• Arbre binaire de recherche
• Arbre AVL
• Arbre bicolore (arbre rouge-noir)
• Arbre cousu

Autres types d'arbres

• Arbre B
• Arbre BSP

Notes et références

• Portail de l'informatique théorique