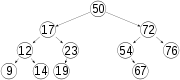
Arbre Andelson-Velskii et Landis

Arbre Andelson-Velskii et Landis: Arbre AVL

Pour les articles homonymes, voir AVL.

Un exemple d'arbre non-AVL.

En informatique, les arbres AVL ont été historiquement les premiers arbres binaires de recherche automatiquement équilibrés. Dans un arbre AVL, les hauteurs des deux sous-arbres d'un même nœud diffèrent au plus de un. La recherche, l'insertion et la suppression sont toutes en O(ln n) dans le pire des cas. L'insertion et la suppression nécessitent d'effectuer des rotations.

La dénomination "arbre AVL" provient des noms de ses deux inventeurs, respectivement G.M. Adelson-Velsky et E.M. Landis, qui l'ont publié en 1962 sous le titre An algorithm for the organization of information.

Le facteur d'équilibrage d'un nœud est la différence entre la hauteur de son sous-arbre droit et celle de son sous-arbre gauche. Un nœud dont le facteur d'équilibrage est 1, 0, ou -1 est considéré comme équilibré. Un nœud avec tout autre facteur est considéré comme déséquilibré et requiert un rééquilibrage. Le facteur d'équilibrage est soit déduit des hauteurs des sous arbres, soit stocké dans chaque nœud de l'arbre (ce qui permet un gain de place, ce facteur pouvant être stocké sur deux bits, mais complexifie les opérations d'insertion et de suppression).

Le même arbre après un rééquilibrage.

Sommaire

1 Opérations

1.1 Insertion

1.2 Suppression

1.3 Recherche

2 Taille

3 Notes et références

3.1 Sources

4 Voir aussi

4.1 Articles connexes

4.2 Liens externes

Opérations

Les opérations de base d'un arbre AVL mettent en œuvre généralement les mêmes algorithmes que pour un arbre binaire de recherche, à ceci près qu'il faut ajouter des rotations de rééquilibrage nommées "rotations AVL".

Insertion

L'insertion dans un arbre AVL se déroule en deux étapes : Tout d'abord, on insère le nœud exactement de la même manière que dans un arbre binaire de recherche ; puis on remonte depuis le nœud inséré vers la racine en effectuant une rotation sur chaque sous-arbre déséquilibré. La hauteur de l'arbre étant en $O (l n (n))$ , et les rotations étant à temps constant, l'insertion se fait finalement en $O (l n (n))$ .

Suppression

La suppression dans un arbre AVL peut se faire par rotations successives du nœud à supprimer jusqu'à une feuille (en choisissant ces rotations de sorte que l'arbre reste équilibré), et ensuite en supprimant cette feuille directement. La suppression se fait aussi en $O (l n (n))$ .

Recherche

La recherche dans un arbre AVL se déroule exactement de la même manière que pour un arbre binaire de recherche, et comme la hauteur d'un arbre AVL est en $O (l n (n))$ , elle se fait donc en $O (l n (n))$ . Contrairement aux arbres splay, la recherche ne modifie pas la structure de l'arbre.

Taille

Dans un arbre AVL de hauteur h, dans le pire des cas, en supposant que l'arbre est déséquilibré vers la gauche, le sous-arbre de gauche aura une hauteur de h-1, tandis que le sous-arbre de droite aura une hauteur de h-2.

Ceci donne une formule de récurrence pour connaître la taille minimale d'un arbre AVL de hauteur h. Cette formule de récurrence est la définition par récurrence des nombres de Fibonacci : $f (n) = f (n - 1) + f (n - 2)$

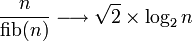
Inversement, dans le meilleur des cas, « le nombre de nœuds internes est égal au logarithme en base deux de la hauteur, diminué de un »^[1]^,^[2] : $\dfrac{n}{\mathrm{fib}(n)} \longrightarrow \sqrt{2} \times \log_{2}{n}$

Cela donne une formule pour calculer la hauteur, dans le pire des cas, pour un arbre AVL contenant n nœuds internes.

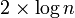
Cette grandeur est meilleure que pour les arbres rouge et noir, où on a^[1]^,^[3] : $2 \times \log{n}$

Notes et références

↑ ^{a et b} Cormen, Leiserson, Introduction à l'algorithmique, annexe B

↑ [pdf] http://www.engr.mun.ca/~theo/Courses/dm/pub/2004/dm-application5.pdf

↑ Pour des informations sur la taille, on pourra aussi consulter la page web {en} http://www.dyalog.dk/dfnsdws/n_avl.htm

Sources

G. Adelson-Velskii et E.M. Landis, « An algorithm for the organization of information ». Doklady Akademii Nauk SSSR, 146 : 263–-266, 1962.

Danièle Beauquier, Jean Berstel, Philippe Chrétienne : Éléments d’algorithmique. Masson, 1992. (ISBN 2-225-82704-4) Voir en particulier le chapitre 6 sur les « arbres et ensembles ordonnées ».

Donald Knuth. The Art of Computer Programming, volume 3 : « Sorting and Searching », 3^e édition. Addison-Wesley, 1997. (ISBN 0-201-89685-0) Voir en particulier les pages 458 à 475 de la section 6.2.3 : « Balanced Trees », expression qui désigne les arbres AVL chez Knuth.

Voir aussi

Articles connexes

Rotation d'un arbre binaire de recherche

Arbre splay

Arbre rouge-noir

Arbre B

Liens externes

(fr)Jean-Jacques Levy, École polytechnique : un cours d'algorithmique.

(en)Université de Mannheim : simulation des arbres AVL.

(en)Université d'Ottawa : applet sur les arbres AVL.

(en)Jorge Riera Ledesma, Université de La Laguna : applet sur les arbres AVL, Splay et rouge-noir.

(en)Navl : classe C# de liste accessible par position et par comparaison de valeur, à base d'« AVL threadé ».

Portail de l’informatique

Ce document provient de « Arbre AVL ».

Catégories : Algorithmique | Arbre (structure de données)