- Nombre tetraedrique
-
Nombre tétraédrique
Un tétraèdre à 35 sphères. Chaque niveau représente un des 5 premiers nombres triangulaires.Un nombre tétraédrique, ou nombre pyramidal triangulaire, est un nombre figuré qui peut être représenté par une pyramide avec une base et trois côtés, c'est-à-dire, un tétraèdre. Pour tout entier naturel non nul n, le nombre tétraédrique de rang n, est la somme des n premiers nombres triangulaires .
On démontre que le nombre tétraédrique de rang n est égal à :
-
,
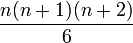- soit
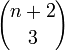, où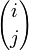 
est le symbole du coefficient binomial.
Les nombres tétraédriques sont donc ceux de la quatrième colonne du triangle de Pascal.
Les premiers nombres tétraédriques sont :
1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969.
Les nombres tétraédriques peuvent être représentés dans l'espace ordinaire de dimension trois. Par exemple, le nombre tétraédrique 35 peut être représenté par un assemblage de 35 boules de billard. Le « triangle » (armature triangulaire standard du jeu de billard) contient 15 boules. Dix boules supplémentaires sont alors empilées au-dessus de celles-ci, ensuite six de plus forment un autre étage, puis encore trois boules et enfin une complètent le tétraèdre.
La parité des nombres tétraédriques suit le modèle impair-pair-pair-pair.
En 1878, A.j. Meyl a démontré qu'il y a seulement trois nombres tétraédriques qui sont également carrés, à savoir, 1, 4 et 19600. Jusqu'ici, le seul nombre tétraédrique connu qui soit aussi un nombre pyramidal carré est 1.
Portail des mathématiques
Catégorie : Nombre figuré -
Wikimedia Foundation. 2010.
