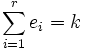Nombre Presque Premier
- Nombre Presque Premier
-
Nombre presque premier
Un nombre entier est dit k-presque-premier, pour k > 0, lorsqu'il est le produit d'exactement k nombres premiers non nécessairement distincts.
Exemple :
- 18 = 2 × 3 × 3.
Donc 18 est un 3-presque-premier.
Définition
Soit un entier 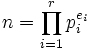 .
.
On dit que n est un k-presque-premier si et seulement si
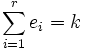
On note alors 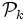 , l'ensemble des k-presque-premiers.
, l'ensemble des k-presque-premiers.
Alors clairement, l'ensemble des nombres premiers, 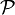 , se confond avec
, se confond avec 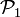 .
.
De même, 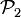 est l'ensemble des nombres semi-premiers.
est l'ensemble des nombres semi-premiers.
L'ensemble 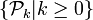 forme une partition de
forme une partition de 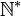 (en convenant que
(en convenant que 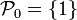 ).
).
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Nombre premier
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Presque Premier de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Nombre presque premier — Un nombre entier est dit k presque premier, pour k > 0, lorsqu il est le produit d exactement k nombres premiers non nécessairement distincts. Exemple : 18 = 2 × 3 × 3. Donc 18 est un 3 presque premier. Définition Soit un entier . On dit… … Wikipédia en Français
Presque premier — Nombre presque premier Un nombre entier est dit k presque premier, pour k > 0, lorsqu il est le produit d exactement k nombres premiers non nécessairement distincts. Exemple : 18 = 2 × 3 × 3. Donc 18 est un 3 presque premier. Définition… … Wikipédia en Français
Nombre Semi-Premier — Un nombre semi premier en mathématiques, aussi appelé bi premier ou 2 presque premier, est un entier naturel qui est le produit de deux nombres premiers pas nécessairement distincts. Les nombres semi premiers sont : 4, 6, 9, 10, 14, 15, 21,… … Wikipédia en Français
Nombre semi-premier — Un nombre semi premier en mathématiques, aussi appelé bi premier ou 2 presque premier, est un entier naturel qui est le produit de deux nombres premiers pas nécessairement distincts. Les nombres semi premiers sont : 4, 6, 9, 10, 14, 15, 21,… … Wikipédia en Français
Nombre Presque Parfait — En mathématiques, un nombre presque parfait (quelquefois appelé aussi nombre légèrement déficient) est un entier naturel n tel que la somme de tous les diviseurs de n (ie. la fonction diviseur ) est égale à 2n 1. Les seuls nombres presque… … Wikipédia en Français
Nombre presque parfait — En mathématiques, un nombre presque parfait (quelquefois appelé aussi nombre légèrement déficient) est un entier naturel n tel que la somme de tous les diviseurs de n (ie. la fonction diviseur ) est égale à 2n 1. Les seuls nombres presque… … Wikipédia en Français
Nombre primaire — Un nombre primaire, également appelé puissance première, est une puissance à exposant entier positif non nul d un nombre premier. Par exemple : 5=51, 9=32 et 16=24 sont des nombres primaires, alors que 6=2×3, 15=3×5 et 36=62=22×32 n en sont… … Wikipédia en Français
premier — premier, ière [ prəmje, jɛr ] adj. et n. • 1104; primer 980; lat. primarius, de primus I ♦ Adj. Qui vient avant les autres, dans un ordre (le plus souvent avant le nom, en épithète). 1 ♦ Qui est le plus ancien ou parmi les plus anciens dans le… … Encyclopédie Universelle
Nombre Parfait — Un nombre parfait est un nombre entier n strictement supérieur à 1 qui est égal à la somme de ses diviseurs stricts, autrement dit, tel que où σ(n) est la somme des diviseurs entiers positifs de n, n non compris. Le premier nombre parfait est 6,… … Wikipédia en Français
Nombre Composé — Un nombre composé est un nombre entier positif qui possède un diviseur positif autre que un ou lui même. Par définition, chaque entier plus grand que un est soit un nombre premier, soit un nombre composé. Les nombres zéro et un ne sont considérés … Wikipédia en Français
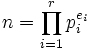 .
.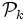 , l'ensemble des k-presque-premiers.
, l'ensemble des k-presque-premiers.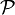 , se confond avec
, se confond avec 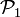 .
.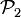 est l'ensemble des nombres semi-premiers.
est l'ensemble des nombres semi-premiers.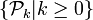 forme une partition de
forme une partition de 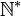 (en convenant que
(en convenant que 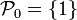 ).
).