Nombre De Keith

Nombre De Keith

Nombre de Keith

En mathématiques, un nombre de Keith ou nombre repfigit est un entier qui apparaît sous forme d'un terme dans une relation de récurrence linéaire comportant les chiffres du nombre initial. Donnons-nous un nombres à n-chiffres

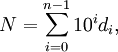
N=\sum_{i=0}^{n-1} 10^i {d_i},

est une suite SN formée avec les termes initiaux 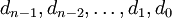d_{n-1}, d_{n-2},\ldots, d_1, d_0 et de terme général produit comme la somme des n termes précédents. Si le nombre N apparaît dans la suite SN, alors N est qualifié nombre de Keith.

Par exemple, prenons 197 : 1 + 9 + 7 = 17 ; 9 + 7 + 17 = 33 ; 7 + 17 + 33 = 57, etc.

On obtient alors la suite : 1, 9, 7, 17, 33, 57, 107, 197, 361... dans laquelle se trouve le nombre 197.

Les premiers petits nombres de Keith sont :

14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909

S'il existe ou pas une infinité de nombres de Keith est actuellement un sujet de spéculation. Il existe seulement 71 nombres de Keith inférieurs à 1019, les rendant beaucoup plus rares que les nombres premiers.

Lien externe

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre de Keith ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre De Keith de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Nombre de keith — En mathématiques, un nombre de Keith ou nombre repfigit est un entier qui apparaît sous forme d un terme dans une relation de récurrence linéaire comportant les chiffres du nombre initial. Donnons nous un nombres à n chiffres est une suite SN… …   Wikipédia en Français

  • Nombre de Keith — En mathématiques, un nombre de Keith ou nombre repfigit est un entier qui apparaît sous forme d un terme dans une relation de récurrence linéaire comportant les chiffres du nombre initial. Etant donné un nombre à n chiffres formons une suite SN… …   Wikipédia en Français

  • Keith Moon — con The Who en el Maple Leaf Gardens, en Toronto, Canadá, en 1976. Datos generales No …   Wikipedia Español

  • Keith Richards — durante una actuación de The Rolling Stones ofrecida en Río de Janeiro. Datos generales Nombre real Keith Richards …   Wikipedia Español

  • Keith Hunter Jesperson — Nombre real Keith Hunter Jesperson Nacimiento 6 de abril de 1955 (55 años) Chilliwack, Columbia Británica, Canadá Alias El Asesino del Rostro Feliz Keith Hunter Jesperson (nacido el 6 de abril de 1955) es un asesino en s …   Wikipedia Español

  • Keith Scott — Keith Scott. Keith Scott, Madrid 2003. Datos generales Nombre real Keith Douglass Scott. Nacimiento …   Wikipedia Español

  • Keith Coogan — Nombre real Keith Eric Mitchell Nacimiento 13 de enero de 1970 41 años …   Wikipedia Español

  • Keith Larsen — Nombre real Keith Eric Burt Nacimiento 17 de junio de 1924 Salt Lake City, Utah, Estados Unidos de América Fallecimiento …   Wikipedia Español

  • Keith Tippett — Datos generales Nombre real Keith Graham Tippetts Nacimiento …   Wikipedia Español

  • Keith Olbermann — en 2008. Nombre real: Keith Theodore Olbermann Nacimiento: 27 de enero de 1959 (52 años) Nueva York …   Wikipedia Español

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”