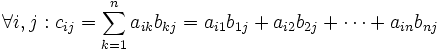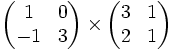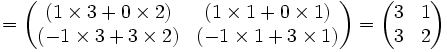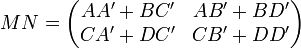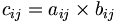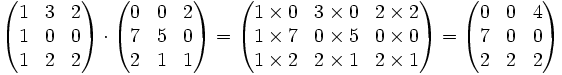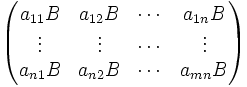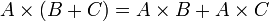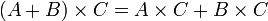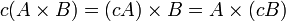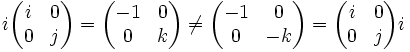- Multiplication de matrices
-
Produit matriciel
Le produit matriciel désigne le produit de matrices, initialement appelé la « composition des tableaux »[1]. Cet article montre comment multiplier les matrices.
Sommaire
Produit matriciel ordinaire
Il s'agit de la façon la plus fréquente de multiplier des matrices entre elles. Le produit de deux matrices ne peut se définir que si le nombre de colonnes de la première matrice est le même que le nombre de lignes de la deuxième matrice, c'est-à-dire lorsqu'elles sont de type compatible.
Si A = (aij) est une matrice de type (m,n) et B = (bij) est une matrice de type (n,p), alors leur produit, noté AB = (cij) est une matrice de type (m,p) donnée par :
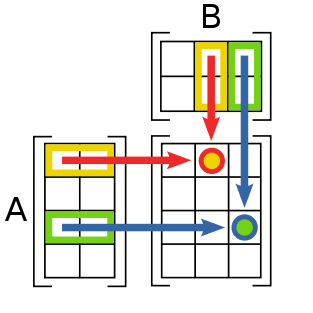
La figure suivante montre comment calculer les coefficients c12 et c33 de la matrice produit AB si A est une matrice de type (3,2), et B est une matrice de type (2,3).
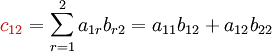
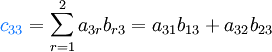
Exemple
Cette notion de multiplication est importante parce que si A et B sont interprétées comme des matrices d'applications linéaires (ce qui est presque toujours le cas), alors la matrice produit AB représente la matrice de la composition des deux applications linéaires, avec celle qui correspond à B qui est appliquée en premier.
En général, la multiplication des matrices n'est pas commutative, c'est-à-dire que AB n'est pas égal à BA.
Multiplication de matrices par bloc
Si l'on considère les matrices
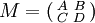 et
et 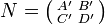 , où A,A',B,B',C,C' et D,D' sont des matrices vérifiant :
, où A,A',B,B',C,C' et D,D' sont des matrices vérifiant :- Le nombre de colonnes de A et C est égal au nombre de lignes de A' et B'
- Le nombre de colonnes de B et D est égal au nombre de lignes de C' et D'
on a alors l'égalité
On remarquera l'analogie entre le produit de matrice par blocs et le produit de deux matrices carrées d'ordre 2.
N.B. : On ne définit pas ainsi une nouvelle forme de multiplication de matrices. Cela correspond simplement à une méthode de calcul du produit matriciel ordinaire pouvant simplifier les calculs.
Produit d'Hadamard
Pour deux matrices de même type, nous avons le produit d'Hadamard ou produit composante par composante. Le produit d'Hadamard de deux matrices A = (aij) et B = (bij) de type (m,n), noté A · B = (cij), est une matrice de type (m,n) donnée par
Par exemple :
Remarquons que le produit d'Hadamard est une sous-matrice du produit de Kronecker (voir ci-dessous). Le produit d'Hadamard est étudié par les théoriciens des matrices, mais n'est pas du tout utilisé par les algébristes linéaires.
Produit de Kronecker
Article détaillé : Produit de Kronecker.Pour deux matrices arbitraires A = (aij) et B, nous avons le produit tensoriel ou produit de Kronecker A ⊗ B qui est défini par
Remarquons que si A est une matrice de type (m,n) et B est une matrice de type (p,r) alors A ⊗ B est une matrice de type (mp,nr). À nouveau cette multiplication n'est pas commutative.
Par exemple
 .
.
Si A et B sont les matrices d'applications linéaires V1 → W1 et V2 → W2, respectivement, alors A ⊗ B représente le produit tensoriel des deux applications, V1 ⊗ V2 → W1 ⊗ W2.
Propriétés communes
Les trois multiplications matricielles précédentes sont associatives
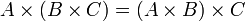 ,
,
distributives par rapport à l'addition :
et compatibles avec la multiplication par un scalaire :
Multiplication par un scalaire
La multiplication par un scalaire r d'une matrice A = (aij) donne le produit
- rA = (raij).
Si nous travaillons avec des matrices sur un anneau, alors la multiplication par un scalaire est parfois appelée la multiplication à gauche tandis que la multiplication à droite est définie par :
- Ar = (aijr).
Quand l'anneau fondamental est commutatif, par exemple, le corps des réels ou des complexes, les deux multiplications sont identiques.
Cependant, si l'anneau n'est pas commutatif, tel que celui des quaternions, alors ils peuvent être différents. Par exemple
Voir aussi
Articles connexes
Notes et références
- ↑ Alain Connes, Triangle de pensées, Edition Odile Jacob, p.72.
Lien externe
- Portail des mathématiques
Catégorie : Matrice
Wikimedia Foundation. 2010.