Mouvement parabolique

Mouvement parabolique

Trajectoire parabolique

Une trajectoire est dite parabolique si le mouvement d'un corps dans l'espace décrit une parabole.

Le mouvement parabolique s'effectue lorsqu'un projectile est soumis à une vitesse initiale et à la seule accélération de la pesanteur. Un exemple courant de mouvement parabolique est l'obus tiré depuis un canon.

La découverte de la trajectoire parabolique est attribuée à Galilée en 1638. Certains historiens des sciences pensent qu'il a été largement influencé par les artistes de son époque qui savaient représenter la trajectoire de l'eau des fontaines.[1]

Sommaire

Exemples

Lorsqu'on lance un objet en l'air, hormis le cas où il a été lancé rigoureusement à la verticale vers le haut, sa trajectoire est une courbe que l'on peut assimiler à une parabole. Par exemple, le tir d'un boulet de canon ou d'une boule de pétanque décrit une trajectoire quasi-parabolique. Les comètes passent au voisinage du Soleil ou de la Terre sur une orbite " parabolique ". Si un avion effectue une trajectoire parabolique, alors les passagers embarqué se trouvent en impesanteur.

Étude de la trajectoire d'un projectile

Le mouvement d'un objet soumis à un champ de pesanteur uniforme (en l'absence de frottements) est une trajectoire parabolique (balistique).

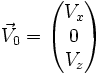
Soit un corps supposé ponctuel de masse m, étudié dans un repère (O, x, y, z), supposé galiléen z étant la verticale, dirigée vers le haut. Ce corps est placé dans un champ de pesanteur, l'accélération de la pesanteur est g. Le corps est lancé depuis le point (x0, y0, z0) avec une vitesse initiale : \vec V_0=\begin{pmatrix} V_x \\ 0 \\ V_z \end{pmatrix}

On suppose ici qu'il n'y a pas de composante de vitesse suivant l'axe 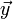\vec y, tout le mouvement a donc lieu dans un plan parallèle au plan (xOz). On note t le temps.

Résolution de l'équation

La seule force à laquelle soit soumis le corps est la gravité (on peut affiner le problème en ajoutant par exemple le frottement dû à l'air). La seule accélération imprimée au corps est donc l'accélération de la pesanteur.

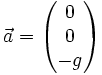
\vec a = \begin{pmatrix}0 \\ 0 \\ -g \end{pmatrix}

Pour en déduire la vitesse, il suffit d'intégrer l'accélération.

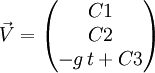
\vec V = \begin{pmatrix}C1 \\ C2 \\ -g\,t+C3 \end{pmatrix}

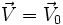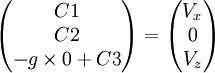C1, C2 et C3 sont des constantes d'intégration, données par les conditions initiales. En effet à t = 0, \vec V = \vec V_0, soit \begin{pmatrix}C1 \\ C2 \\ -g\times 0+C3 \end{pmatrix} = \begin{pmatrix} V_x \\ 0 \\ V_z \end{pmatrix},

d'où C1 = Vx, C2 = 0 et C3=Vz.

On a donc

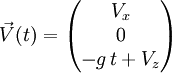
\vec V(t) = \begin{pmatrix}V_x \\ 0 \\ -g\,t+V_z \end{pmatrix}

Pour obtenir l'équation de la trajectoire, il faut intégrer la vitesse.

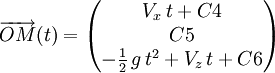
\overrightarrow{OM}(t)=\begin{pmatrix}V_x\,t+C4 \\ C5 \\ -{1 \over 2}\,g\,t^2+V_z\,t+C6 \end{pmatrix}

C4, C5 et C6 sont (à nouveau) des constantes d'intégration qui seront déterminées à l'aide des conditions initiales.

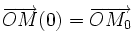
A t = 0, \overrightarrow{OM}(0)= \overrightarrow{OM_0}

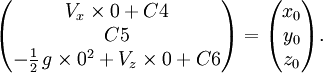
Donc \begin{pmatrix}V_x\times 0+C4 \\ C5 \\ -{1 \over 2}\,g\times 0^2+V_z\times 0+C6 \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix}.
d'où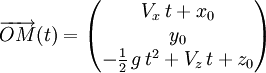 \overrightarrow{OM}(t) = \begin{pmatrix}V_x\,t+x_0 \\ y_0 \\ -{1 \over 2}\,g\,t^2+V_z\,t+z_0 \end{pmatrix}

Équation de la trajectoire

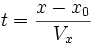
On peut donner l'équation sous la forme z = f(x) (z est une fonction de x ) en remplaçant t dans l'équation de z par l'expression qu'on en tire dans l'équation de x, soit t={x-x_0 \over V_x}

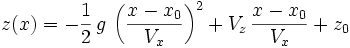
On obtient donc : z(x) = - {1 \over 2}\,g\,\left({x-x_0 \over V_x}\right)^2+V_z\,{x-x_0 \over V_x}+z_0

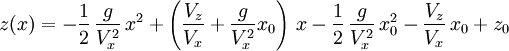
z(x) = -{1 \over 2}\,{g \over V_x^2}\,x^2+\left({V_z \over V_x } + {g \over V_x^2}x_0\right)\,x-{1 \over 2}\,{g \over V_x^2}\,x_0^2-{V_z \over V_x}\,x_0+z_0

L'équation de ce mouvement indique bien la parabole qui donne son nom à ce mouvement. Cette équation permet aussi de retirer plusieurs informations utile comme par exemple les endroits ou le projectile touche le sol (résoudre l'équation z(x) = 0 ).

Graphique

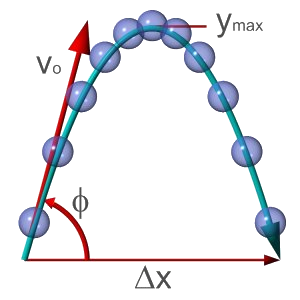
exemple d'un tir parabolique

Ici φ est l'angle que fait le vecteur vitesse initiale avec l'horizontale :
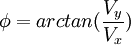
\phi = arctan(\frac{V_y}{V_x})


Notes et références de l'article

Voir aussi

Articles connexes

Liens et documents externes

  • Portail de la physique Portail de la physique
Ce document provient de « Trajectoire parabolique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Mouvement parabolique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Mouvement parabolique — ● Mouvement parabolique mouvement, selon un arc de parabole, d un point matériel soumis à une force constante …   Encyclopédie Universelle

  • mouvement parabolique — parabolinis judėjimas statusas T sritis fizika atitikmenys: angl. parabolic motion vok. Parabelbewegung, f rus. параболическое движение, n pranc. mouvement parabolique, m …   Fizikos terminų žodynas

  • parabolique — 1. parabolique [ parabɔlik ] adj. • v. 1500; lat. ecclés. parabolicus ♦ Rare Relatif à la parabole (1.). ⇒ allégorique. parabolique 2. parabolique [ parabɔlik ] adj. • 1571; de 2. parabole 1 ♦ Relatif à la parabole (2.). ♢ En forme de parabole.… …   Encyclopédie Universelle

  • Mouvement harmonique simple — Oscillateur harmonique Un oscillateur harmonique est un oscillateur dont l évolution au cours du temps est décrite par une fonction sinusoïdale et dont la fréquence ne dépend que des caractéristiques du système. L intérêt d un tel modèle est qu… …   Wikipédia en Français

  • Trajectoire parabolique — Une trajectoire est dite parabolique si le mouvement d un corps dans l espace décrit une parabole. Le mouvement parabolique s effectue lorsqu un projectile est soumis à une vitesse initiale et à la seule accélération de la pesanteur. Un exemple… …   Wikipédia en Français

  • Équation de Kepler — En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer des paramètres dynamiques du mouvement d un astre (l… …   Wikipédia en Français

  • Equation de Kepler — Équation de Kepler En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer de paramètres dynamiques du mouvement d… …   Wikipédia en Français

  • Équation de kepler — En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer de paramètres dynamiques du mouvement d un astre (l… …   Wikipédia en Français

  • EULER (L.) — Avec Joseph Louis Lagrange, son émule plus jeune, Leonhard Euler est l’un des deux géants mathématiques qui ont dominé la science du XVIIIe siècle. Ses travaux, d’une abondance inégalée, couvrent tout le champ des mathématiques, de la mécanique… …   Encyclopédie Universelle

  • Parabelbewegung — parabolinis judėjimas statusas T sritis fizika atitikmenys: angl. parabolic motion vok. Parabelbewegung, f rus. параболическое движение, n pranc. mouvement parabolique, m …   Fizikos terminų žodynas

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”