- Modèle semi-classique
-
Modèle de Bohr
Pour consulter un article plus général, voir : atome.Le modèle de Bohr est une théorie physique, basée sur le modèle planétaire de Rutherford cherchant à comprendre la constitution d'un atome, et plus particulièrement, celui de l'hydrogène et des ions hydrogénoïdes (ions ne possédant qu'un seul électron).
Sommaire
Principe
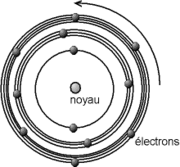
Ce modèle est un complément du modèle planétaire d'Ernest Rutherford qui décrit l'atome d'hydrogène comme un noyau massif et chargé positivement, autour duquel se déplace un électron chargé négativement.
Le problème posé par ce modèle est que l'électron, charge électrique accélérée, devrait selon la physique classique, rayonner de l'énergie et donc finir par s'écraser sur le noyau.
Niels Bohr propose d'ajouter deux contraintes :
- L'électron ne rayonne aucune énergie lorsqu'il se trouve sur une orbite stable (ou orbite stationnaire). Ces orbites stables sont différenciées, quantifiées. Ce sont les seules orbites sur lesquelles l'électron peut tourner.
- L'électron ne rayonne ou n'absorbe de l'énergie que lors d'un changement d'orbite.
Pour commodité de lecture, les orbites possibles de l'électron sont représentées dans la littérature comme des cercles de diamètres quantifiés (Cette théorie est un modèle qui n'existe pas dans la réalité, il n'existe pas de position ni de vitesse précise d'un électron, et il ne peut donc parcourir un "cercle"; son orbitale peut en revanche être parfois sphérique).
Théorie
L'atome d'hydrogène est modélisé par un électron de masse m tournant autour du proton.
L'énergie mécanique
L'interaction entre ces deux particules est électrostatique: la force intervenant est la force de Coulomb. Ceci nous permet donc d'écrire l'énergie potentielle de l'électron à une distance r du noyau :
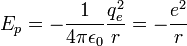
- ε0 est la permittivité du vide
- qe est la charge de l'électron
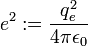 , par souci de simplification d'écriture ( cf système d'unités atomiques ).
, par souci de simplification d'écriture ( cf système d'unités atomiques ).
D'autre part, comme il est question d'un mouvement à force centrale, l'accélération de cet électron vaut
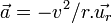 où v est la vitesse de l'électron, et
où v est la vitesse de l'électron, et 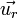 est le vecteur unitaire centrifuge. Le principe fondamental de la dynamique implique alors :
est le vecteur unitaire centrifuge. Le principe fondamental de la dynamique implique alors :
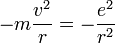
On peut alors calculer l'énergie cinétique :
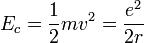
Finalement, on obtient l'énergie mécanique :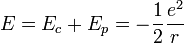
Quantification
Ici intervient alors la quantification du moment cinétique
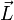 : selon l'hypothèse de Bohr :
: selon l'hypothèse de Bohr :
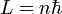 où n est un entier positif non nul, et
où n est un entier positif non nul, et 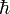 est la constante de Planck "réduite" ( d'un facteur 2 π).
est la constante de Planck "réduite" ( d'un facteur 2 π).
: seules les orbites ayant ce moment cinétique ne rayonnent pas : les orbites sont donc "quantifiées" par le nombre entier n positif. Cette relation s'écrit :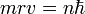
Cette quantification a été confirmée par l'expérience de Franck et Hertz. L'intérêt de cette expérience est de montrer que la quantification n'est pas seulement due à la quantification de la lumière, mais bien à la quantification de l'orbite des électrons présents dans l'atome.
Résultats
- Les deux équations précédentes:
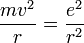 et
et 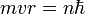
permettent de calculer la distance entre le noyau et l'électron, r ( ainsi que la vitesse v ):
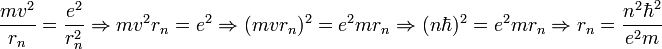
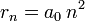
- où
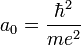 est le rayon de Bohr, soit environ 53 pm.
est le rayon de Bohr, soit environ 53 pm.
- L'énergie totale de l'électron est aussi quantifiée :
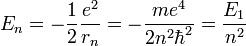
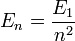
avec
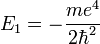
- E1 est une unité d'énergie, appelée énergie de Rydberg (cf constante de Rydberg), et vaut environ -13.6 eV.
- Néanmoins cette théorie, même modifiée par Sommerfeld pour tenir compte des orbites elliptiques, ne survivra pas à la révolution de la mécanique quantique en 1926.
Note historique
Durant les XVIIIe et XIXe siècles, on mesure, par spectroscopie, des spectres de différentes sources lumineuses comme le soleil ou la lampe à hydrogène. Depuis Thomas Melvill (1726-1753) en 1750, on a observé que ces spectres sont formés de raies.
La spectroscopie théorique naît avec les lois de Bunsen (1811-1899) et de Kirchhoff (1824-1887) publiées en 1859. Niels Bohr (1885-1962) est le premier à pouvoir expliquer ce phénomène de quantification en 1913.
Il avait été guidé par l'expression simple d'une formule (dite de Balmer), qui associe les fréquences des raies composant le spectre de l'hydrogène, à la différence entre deux termes d'énergie. En effet, Balmer (1825-1898) trouva empiriquement la relation donnant les longueurs d'onde des raies :
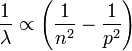 en accord avec les raies trouvées dans le visible par Ångström et dans l'ultra-violet par Huggins. Cela a permis de décrire l'atome comme émettant ou absorbant une certaine quantité d'énergie quantifiée (le photon).
en accord avec les raies trouvées dans le visible par Ångström et dans l'ultra-violet par Huggins. Cela a permis de décrire l'atome comme émettant ou absorbant une certaine quantité d'énergie quantifiée (le photon).Or la théorie planétaire de Rutherford de 1911 se heurtait à la théorie du rayonnement de l'électron accéléré. En effet, cet électron émettait de l'énergie et devait s'écraser sur le noyau au bout de quelques millions de révolutions, ce qui correspond à une nanoseconde.
En 1913, Bohr a introduit ses deux postulats pour rendre le modèle compatible avec ces observations. Il suppose que l'électron parcourt différentes orbites circulaires quantifiées autour du noyau : lorsque l'électron change d'orbite, un photon transportant de l'énergie est émis. Les orbites deviennent donc niveaux d'énergie. Le spectre atomique de l'hydrogène, et le problème du modèle de Rutherford étaient ainsi expliqués.
Niels Bohr publia alors en juillet 1913 son article : On the constitution of atoms and molecules, Philosophical Magazine, series 6, vol. 26, July 1913,p 1-25. Dans celui-ci, il explique pourquoi, après les expériences de Geiger (1913), il opte pour l'atome planétaire de Rutherford (1911) contre l'atome de Thomson (1904). Il indique qu'il est redevable à Planck de la notion de quanta et de la constante de Planck. Il reconnaît à l'astronome Nicholson (1912) l'idée de considérer le moment cinétique.
Remarques et conséquences
La formule de Balmer ne satisfait pas Bohr dans la mesure où cette longueur d'onde est monochromatique, et ne correspond à aucune oscillation de l'électron : il n'y a pas de résonance.
D'autre part, il n'y a pas de référence à la masse réduite dans cet article, alors qu'elle est souvent présentée comme un succès pour expliquer le passage de la constante de Rydberg théorique R∞ à la constante de Rydberg pour l'atome d'hydrogène RH.
Toutefois, l'énigme de l'hydrogène de Pickering, moins citée, a pu être résolue : l'astronome Pickering publie des séries de raies qui s'accordent avec la théorie de Rydberg, mais en prenant n et m demi-entiers (1895). Fowler le confirme (Décembre 1912) dans une expérience terrestre avec un tube contenant de l'hydrogène et de l'hélium. Bohr a alors l'idée de la réaction suivante: H + He → H– + He+, et déclare que l'on voit le spectre de l'ion hydrogénoïde He+ (avec une constante de Rydberg quadruple) et que l'hydrogène de Pickering n'existe pas. De plus, il interprète alors les raies des alcalins avec des modifications légères des termes de Ritz par des entiers effectifs.
Néanmoins sa théorie ne permet d'interpréter ni le spectre des autres atomes ni celui des molécules.
Pour la théorie de l'état s de l'hydrogène, il faudra attendre 1926 et l'apparition du principe d'incertitude.
Voir aussi
- Spectre de l'hydrogène
- Expérience de Franck et Hertz
- Constante de Rydberg, formule de Rydberg pour l'explication en mécanique quantique,
- Atome d'hydrogène
- Niels Bohr
- Rayon de Bohr
- Saturation des inégalités d'Heisenberg
- Système d'unités atomiques
- Quantification semi-classique
- Régime semi-classique
- Portail de la physique
- Portail de la chimie
Catégories : Article à recycler (physique) | Atome
Wikimedia Foundation. 2010.