Mesure De Dispersion

Mesure de dispersion

Pour les articles homonymes, voir DM.

La mesure de dispersion (dispersion measure ou DM) est, en astronomie, une quantité intervenant dans l'observation des pulsars, et qui traduit le décalage des temps d'arrivée des signaux émis par ceux-ci en fonction de leur fréquence.

Sommaire

1 Formule
2 Contexte d'utilisation
3 Utilisation de la mesure de dispersion
4 Difficultés de détection des pulsars lointains
5 Note
6 Références

Formule

La mesure de dispersion, souvent notée DM (du fait de l'anglais dispersion measure), correspond au produit de la densité moyenne d'électrons libres $n e$ sur la ligne de visée par la distance L à l'objet observé :

DM = n e L

D'un point de vue d'analyse dimensionnelle, la mesure de dispersion correspond donc à l'inverse d'une surface. Dans le système international d'unités, elle est exprimée en mètre^-2, quoique en pratique on la voit souvent exprimée en parsec par centimètre cube, réminiscence du fait que les distances en astronomie sont usuellement exprimées en parsecs et que les densités le sont souvent dans le système cgs, soit en centimètre^-3.

Contexte d'utilisation

L'utilisation du concept de mesure de dispersion vient du fait que les lois de l'électromagnétisme indiquent que la propagation d'une onde électromagnétique de longueur d'onde $λ$ dans un plasma peu dense s'effectue à la vitesse de groupe v_g donnée par

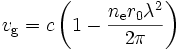$v_{\mathrm{g}} = c \left(1 - \frac{n_{\mathrm{e}} r_0 \lambda^2}{2 \pi} \right)$ ,

où c est le vitesse de la lumière, $n e$ la densité d'électrons libre, $r 0$ le rayon classique de l'électron, $λ$ .

Le retard de temps d'arrivée d'un signal issu d'une source à distance L par rapport au cas où il se propagerait dans le vide est donc

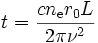$t = \frac{c n_{\mathrm{e}} r_0 L}{2 \pi \nu^2}$ ,

$ν$ étant la fréquence du signal. L'application numérique donne alors, si on exprime ce temps en secondes, et en remplaçant par la définition de la mesure de dispersion,

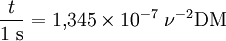$\frac{t}{1 \;{\mathrm{s}}} = 1,\!345 \times 10^{-7} \; \nu^{-2} {\mathrm{DM}}$ .

En utilisant des unités plus appropriées pour le problème, à savoir parsec par centimètre cube pour la mesure de dispersion (voir ci-dessus) et la fréquence en mégahertz (les observations des pulsars se faisant le plus souvent dans le domaine des ondes radio), on obtient

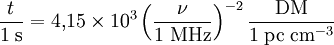$\frac{t}{1 \;{\mathrm{s}}} = 4,\!15 \times 10^{3} \left(\frac{\nu}{1 \; {\mathrm{MHz}}}\right)^{-2} \frac{{\mathrm{DM}}}{1\;{\mathrm{pc}}\;{\mathrm{cm}}^{-3}}$ .

Utilisation de la mesure de dispersion

La relation simple entre mesure de dispersion, densité électronique et distance est utilisée dans les deux sens : dans le cas où la distance au pulsar est bien connue (comme pour le pulsar du Crabe, ou plus généralement les pulsars dont la distance peut être estimée de façon précise, comme par la donnée de leur parallaxe), la donnée de la mesure de dispersion permet de mesurer directement la densité électronique ; dans le cas où la distance n'est pas connue, on utilise la densité électronique mesurée par les méthodes précédentes dans des situations semblables (localisation proche entre le pulsar étudié et celui dont on connaît la distance, par exemple) pour estimer la distance.

Difficultés de détection des pulsars lointains

En pratique, un récepteur radio opère à une certaine fréquence nominale et avec une certaine largeur de bande centrée sur cette fréquence. Pour pouvoir détecter le pulsar proprement dit, il est a priori nécessaire d'observer une modulation périodique du signal observé. Cela ne peut se faire que si le décalage des temps d'arrivée des plus hautes et plus basses fréquences de la bande est inférieur à la période de modulation du signal du pulsar (c'est-à-dire sa période de rotation). Cette différence de temps d'arrivée peut s'écrire, en notant B la largeur de bande du récepteur,

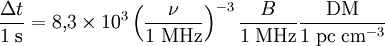$\frac{\Delta t}{1 \;{\mathrm{s}}} = 8,\!3 \times 10^{3} \left(\frac{\nu}{1 \; {\mathrm{MHz}}}\right)^{-3} \frac{B}{1 \; {\mathrm{MHz}}} \frac{{\mathrm{DM}}}{1\;{\mathrm{pc}}\;{\mathrm{cm}}^{-3}}$ .

Pour le pulsar du Crabe, dont la mesure de dispersion est de 57 pc / cm³, un récepteur à 408 MHz donne

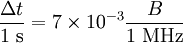$\frac{\Delta t}{1 \;{\mathrm{s}}} = 7 \times 10^{-3} \frac{B}{1 \; {\mathrm{MHz}}}$ .

La période du pulsar étant de 33 millisecondes, il est nécessaire d'avoir une largeur de bande très faible (moins de 5 MHz) pour pouvoir détecter la périodicité du signal du pulsar^[1]. Pour cette raison, les pulsars à rotation très rapide (pulsars millisecondes) sont particulièrement difficiles à détecter et nécessitent des techniques plus spécifiques que la simple périodicité d'un signal dans une bande de fréquence.

Note

↑ En pratique, du fait que la durée de l'impulsion est une fraction significative de la prériode de rotation, cette valeur est largement surestimée.

Références

(en) Andrew G. Lyne & Francis Graham Smith, Pulsar astronomy, Cambridge University Press, 1^re édition, 274 pages (1990) (ISBN 0-521-32681-8), page 27 et 28.

Portail de l’astronomie

Ce document provient de « Mesure de dispersion ».

Catégorie : Pulsar

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Mesure De Dispersion de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Mesure de dispersion — Pour les articles homonymes, voir DM. La mesure de dispersion (dispersion measure ou DM) est, en astronomie, une quantité intervenant dans l observation des pulsars, et qui traduit le décalage des temps d arrivée des signaux émis par ceux ci en… … Wikipédia en Français
mesure de dispersion — sklaidos matas statusas T sritis fizika atitikmenys: angl. measure of dispersion vok. Dispersionsmaß, n; Streuungsmaß, n rus. мера дисперсии, f; мера разброса, f; мера рассеяния, f pranc. mesure de dispersion, f … Fizikos terminų žodynas
MESURE - Méthodologie — L’expérimentation fournit à la recherche scientifique et au contrôle industriel un appui particulièrement efficace. Sa mise en œuvre rationnelle ouvre la voie à la description quantitative des phénomènes, à la vérification de certains postulats… … Encyclopédie Universelle
MESURE - Mesures électriques et électroniques — Les mesures électriques et électroniques, grâce à l’apport des semiconducteurs, des méthodes numériques et des systèmes asservis, apparaissent à l’heure actuelle comme une technique clé dans le domaine des mesures en général. L’existence de… … Encyclopédie Universelle
MESURE - Mesures acoustiques — Le caractère interdisciplinaire de l’acoustique se traduit par des recherches et des mesures dans de nombreux domaines: physique, chimie, électricité, mécanique, aéronautique, propagation sous marine, psychologie, biologie, sciences de la… … Encyclopédie Universelle
MESURE - Mesures optiques — Par mesures optiques, il faut entendre les mesures faites grâce à la lumière. En ce qui concerne les mesures faites sur la lumière, le lecteur se reportera aux rubriques PHOTOMÉTRIE, pour les mesures d’énergie, SPECTROSCOPIE, pour les mesures de… … Encyclopédie Universelle
Dispersion statistique — La dispersion représente la variabilité ou l étendue des différentes valeurs que peut prendre une variable. En statistiques, il existe différentes mesure de la dispersion. Les plus courantes sont : la variance, l écart type ou encore l écart … Wikipédia en Français
Dispersion chromatique — Article principal : Dispersion. Dans les fibres optiques, la dispersion chromatique, correspondant aux variations de temps de propagation des diverses longueurs d onde, est l un des facteurs limitant de la bande passante (l autre étant la… … Wikipédia en Français
Dispersion (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En optique, la vitesse de la lumière dans le vide ne dépend pas de sa longueur d onde, mais dans certains milieux, elle peut en dépendre : c est le… … Wikipédia en Français
dispersion des résultats de mesure — matavimo rezultatų sklaida statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio tam tikros matavimų sekos rezultatų nesutaptis. atitikmenys: angl. dispersion of measuring results rus. рассеяние результатов измерений, n pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Dictionnaires et Encyclopédies sur 'Academic'

Mesure De Dispersion