Anova

Analyse de la variance

L'analyse de la variance (terme souvent abrégé par le terme anglais ANOVA : ANalysis Of VAriance) est un test statistique permettant de vérifier que plusieurs échantillons sont issus d'une même population.

Ce test s'applique lorsque que l'on mesure une ou plusieurs variables explicatives discrètes (appelées alors facteurs de variabilités, leurs différentes modalités étant appelées "niveaux") qui influence sur la distribution d'une variable continue à expliquer. On parle d'analyse à un facteur, lorsque l'analyse porte sur un modèle décrit par un facteur de variabilité, d'analyse à deux facteurs ou d'analyse multifactorielle.

Sommaire

1 Principe
2 Analyse de la variance à un facteur
3 Analyse de la variance à deux facteurs
- 3.1 Décomposition de la variance
- 3.2 Exemple illustratif
4 Analyse de la variance multifactorielle
- 4.1 Décomposition de la variance
5 Limites d'utilisation de l'analyse de la variance
6 Voir aussi
7 Sources
- 7.1 Références

Principe

Notons $Y$ la variable à expliquer continue, $i$ l'indice identifiant l'individu et $X i$ les facteurs de variabilités discrets.

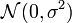On suppose que les facteurs de variabilités $x i$ influencent uniquement les moyennes des distributions et que leurs variances restent identiques (hypothèse d'homoscédasticité) et constantes : chaque facteur $y i$ suit une loi normale $\mathcal{N}(0, \sigma^2)$ .

L'hypothèse nulle correspond au cas où les distributions suivent la même loi normale. L'hypothèse alternative est qu'il existe au moins une distribution dont la moyenne s'écarte des autres moyennes :

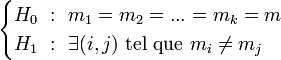$\begin{cases} {H_0~:~m_{1}=m_{2}=...=m_{k}=m} \\ {H_1~:~\exists (i,j)~\text{tel que}~m_i \neq m_j} \end{cases}$ .

Décomposition de la variance

La première étape de l'analyse de la variance consiste à expliquer la variance totale à expliquer sur l'ensemble des échantillons en fonction de la variance due aux facteurs (la variance expliquée par le modèle), de la variance due à l'interaction entre les facteurs et de la variance résiduelle aléatoire (la variance non expliquée par le modèle). 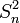$S_n^2$ étant un estimateur biaisé de la variance, on utilise la somme des carrés des écarts (SCE en français, SS pour Sum Square en anglais) pour les calculs et l'estimateur non biaisé de la variance 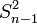$S_{n-1}^2$ (également appelé carré moyen ou CM).

L'écart (sous entendu l'écart à la moyenne) d'une mesure est la différence entre cette mesure et la moyenne :

$e = y_i - \overline{y}$ .

La somme des carrés des écarts SCE et l'estimateur 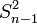$S_{n-1}^2$ se calculent à partir des formules :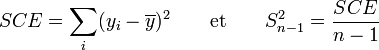

$SCE = \sum_i (y_i - \overline{y})^2 \qquad \text{et} \qquad S_{n-1}^2 = \frac{SCE}{n-1}$

Cette décomposition de la variance est toujours valable, même si les variables ne suivent pas de loi normale.

Test de Fisher

Degrés de liberté et variances

Par hypothèse, la variable observée $y i$ suit une loi normale. La loi du χ² à $k$ degrés de liberté étant définie comme étant la somme de $k$ lois normales au carré, les sommes des carrés des écarts $S C E$ suivent des lois du χ², avec $D D L$ le nombre de degrés de liberté :

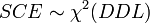
$SCE \sim \chi^2(DDL)~$

La loi de Fisher est définie comme le rapport de deux lois du χ². Dans le cas de l'hypothèse nulle $H 0$ , le rapport entre deux estimateurs non biaisés de la variance 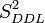$S_{DDL}^2~$ doit donc suivre une Loi de Fisher :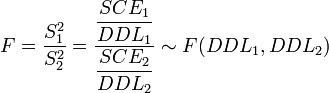

$F = \frac {S^2_1} {S^2_2} = \frac {\dfrac {SCE_1} {DDL_1}} {\dfrac {SCE_2} {DDL_2}} \sim F(DDL_1, DDL_2)$

Si la valeur de $F$ n'est pas compatible avec cette loi de Fisher (c'est-à-dire que la valeur de $F$ est supérieure au seuil de rejet), alors on rejette l'hypothèse nulle : on conclut qu'il existe une différence statistiquement significative entre les distributions. Le facteur de variabilité ne sépare pas la population étudiée en groupes identiques. Pour rappel, la valeur de seuil de rejet $F α (D D L 1, D D L 2)$ est précalculée dans les tables de référence, en fonction du risque de première espèce $α$ et des deux degrés de libertés $D D l 1$ et $D D L 2$ .

Remarques

L'idée de l'analyse de la variance repose sur un modèle qu'on se donne a priori des données. On s'attache ensuite à l'étude de la contribution de ces différents termes à la variance de Y, grâce à une décomposition dite de « l'analyse de la variance ».

Il est important de comprendre que l'analyse de la variance n'est pas un test permettant de « classer » des moyennes par exemple. Comme on l'a noté précédemment, l'hypothèse nulle H0 revient à dire que toutes les moyennes sont égales. Le but ici est donc beaucoup plus « humble » : il s'agit de comparer des moyennes de différents groupes et de dire si, parmi l'ensemble, au moins une d'entre elles diffère des autres, mais on ne sait ni laquelle ni combien d'entre elles. Déterminer quel groupe a un effet différentiel, c’est-à-dire quel groupe présente une moyenne de la variable étudiée différente des autres, est un problème tout à fait différent. Il peut se poser après une ANOVA et les tests associés sont dits « tests de comparaisons multiples », ou MCP pour Multiple Comparison Test. Ces tests obligent en général à augmenter les risques de l'analyse (en termes de risque statistique). Dans la biologie moderne, notamment, des tests MCP permettent de prendre en compte le risque de façon correcte malgré le grand nombre de tests effectués (par exemple pour l'analyse de biopuces). On pourra se reporter notamment aux procédures de Bonferonni et de Sidak.

Il s'agit d'une généralisation à k populations du test T de Student de comparaison de moyennes de deux échantillons.

Analyse de la variance à un facteur

Également appelé one-way ANOVA (en), l'analyse de la variance à un facteur s'applique lorsque l'on souhaite prendre en compte un seul facteur de variabilité.

Décomposition de la variance

Soit un facteur de variabilité pouvant prendre les niveaux $i = 1.. p$ , $n i$ le nombre d'individu dans chaque niveau et $n$ le nombre d'individu total. La variable à expliquer s'écrit 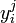$y_i^j$ avec $i = 1.. p$ et $j = 1.. n i$ .

La variable à expliquer peut être modélisée par la relation :

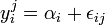
$y_i^j = \alpha_i + \epsilon_{ij} ~$

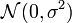avec $α i$ l'effet du niveau $i$ du facteur et $ε i j$ l'erreur aléatoire (qui suit alors une loi normale $\mathcal{N}(0, \sigma^2)$ ).

Dans ces conditions, on montre que la somme des carrés des écarts (et donc la variance) peut être calculée simplement par la formule :

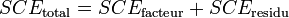
$SCE_\text{total} = SCE_\text{facteur} + SCE_\text{residu} ~$

La part de la variance totale $S C E total$ qui peut être expliquée par le modèle ( $S C E facteur$ , aussi appelée variabilité inter-classe, SSB ou Sum of Square Between class) et la part de la variance totale $S C E total$ qui ne peut être expliquée par le modèle ( $S C E residu$ aussi appelée variabilité aléatoire, variabilité intra-classe, bruit, SSW ou Sum of Square Within class) sont données par les formules :

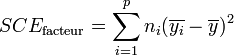
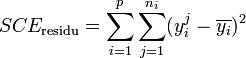$SCE_\text{facteur} = \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2$ $SCE_\text{residu} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2$

Démonstration

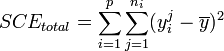$SCE_{total} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y})^2$ .

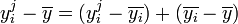En décomposant $~ y_i^j - \overline{y} = (y_i^j - \overline{y_i}) + (\overline{y_i} - \overline{y})$ ,

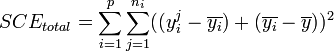
on peut écrire $~ SCE_{total} = \sum_{i=1}^p \sum_{j=1}^{n_i} ((y_i^j - \overline{y_i}) + (\overline{y_i} - \overline{y}))^2$

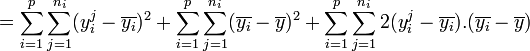$= \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2 + \sum_{i=1}^p \sum_{j=1}^{n_i} (\overline{y_i} - \overline{y})^2 + \sum_{i=1}^p \sum_{j=1}^{n_i} 2( y_i^j - \overline{y_i}).(\overline{y_i} - \overline{y})$ .

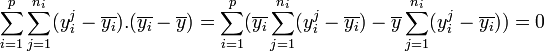En remarquant que $~ \sum_{i=1}^p \sum_{j=1}^{n_i} ( y_i^j - \overline{y_i}).(\overline{y_i} - \overline{y}) = \sum_{i=1}^p (\overline{y_i} \sum_{j=1}^{n_i} (y_i^j - \overline{y_i}) - \overline{y} \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})) = 0$ ,

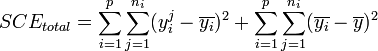
on peut écrire $~ SCE_{total} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2 + \sum_{i=1}^p \sum_{j=1}^{n_i} (\overline{y_i} - \overline{y})^2$

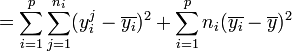
$= \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2 + \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2$

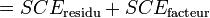$= SCE_\text{residu} + SCE_\text{facteur} ~$ .

Analyse des résidus

Il est toujours possible que le modèle ne soit pas correct et qu'il existe un facteur de variabilité inconnu (ou supposé à priori inutile) qui ne soit pas intégré dans le modèle. Il est possible d'analyser la normalité de la distribution des résidus pour rechercher ce type de biais. Les résidus, dans le modèle, doivent suivre une loi normale 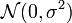$\mathcal{N}(0, \sigma^2)~$ ). Tout écart significatif par rapport à cette loi normale peut être testé ou visualisé graphiquement :

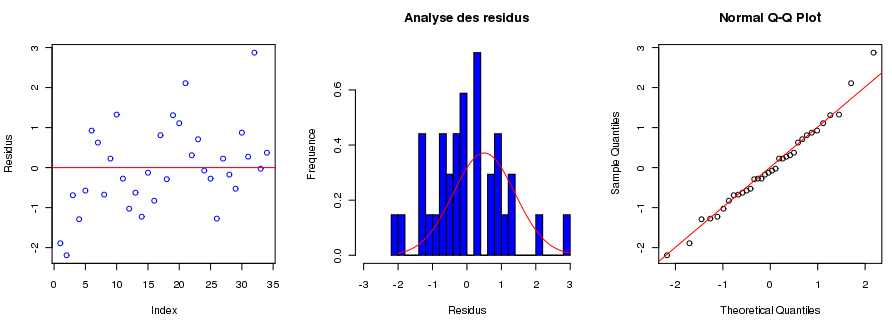Script R

layout(matrix(1:3, 1, 3))

produc <- c(20.1, 19.8, 21.3, 20.7, 22.6, 24.1, 23.8, 22.5, 23.4, 24.5, 22.9, 31.2, 31.6, 31.0, 32.1, 31.4, 22.8, 21.7, 23.3, 23.1, 24.1, 22.3, 22.7, 23.1, 22.9, 21.9, 23.4, 23.0, 31.7, 33.1, 32.5, 35.1, 32.2, 32.6)

race <- as.factor(c("A", "A", "A", "A", "B", "B", "B", "B", "B", "B", "B", "C", "C", "C", "C", "C", "A", "A", "A", "A", "A", "A", "A", "B", "B", "B", "B", "B", "C", "C", "C", "C", "C", "C"))

plot(residuals(lm(produc~race)), ylab="Residus", col="blue")

abline(0, 0, col="red")

hist(residuals(lm(produc~race)), nclass=20, xlab="Residus", ylab="Frequence", xlim=c(-3,3), pro=T, col="blue", main="Analyse des residus")

lines(seq(-3,3,le=100), dnorm(seq(-3,3,le=100), 0, sqrt(var(residuals(lm(produc~race))))), col="red")

qqnorm(residuals(lm(produc~race)))

qqline(residuals(lm(produc~race)), col="red")

Article détaillé : Tests de normalité.

Test de Fisher

Degrés de liberté et variances

Par hypothèse, la variable observée $y i$ suit une loi normale. La loi du χ² à $k$ degrés de liberté étant définit comme étant la somme de $k$ lois normales au carré, les sommes des carrés des écarts $S C E$ suivent les lois du χ² suivantes, avec $p$ le nombre de niveaux du facteur de variabilité et $n$ le nombre total d'individu :

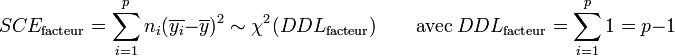
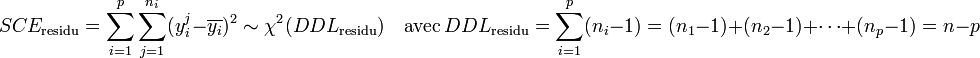
$SCE_\text{facteur} = \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2 \sim \chi^2(DDL_\text{facteur}) \qquad \text{avec} ~ DDL_\text{facteur} = \sum_{i=1}^p 1 = p - 1$ $SCE_\text{residu} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2 \sim \chi^2(DDL_\text{residu}) \quad \text{avec} ~ DDL_\text{residu} = \sum_{i=1}^p (n_i - 1) = (n_1-1)+(n_2-1)+\cdots+(n_p-1) = n - p$

Les variances s'obtiennent en faisant le rapport de la somme des carrés des écarts sur le nombre de degrés de liberté :

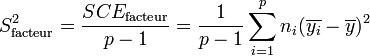
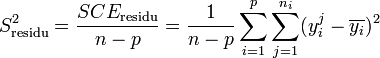
$S^2_\text{facteur} = \frac {SCE_\text{facteur}} {p-1} = \frac 1 {p-1} \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2$ $S^2_\text{residu} = \frac {SCE_\text{residu}} {n-p} = \frac 1 {n-p} \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2$

La Loi de Fisher étant défini comme le rapport de deux lois du χ², le rapport 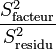$\frac {S^2_\text{facteur}} {S^2_\text{residu}}$ soit donc une Loi de Fisher :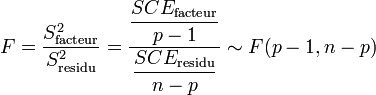

$F = \frac {S^2_\text{facteur}} {S^2_\text{residu}} = \frac {\dfrac {SCE_\text{facteur}} {p-1}} {\dfrac {SCE_\text{residu}} {n-p}} \sim F(p-1, n-p)$

Remarque

Pour les amateurs de géométrie vectorielle, la décomposition des degrés de liberté correspond à la décomposition d'un espace vectoriel de dimension nm en sous espaces supplémentaires et orthogonaux de dimensions respectives $m - 1$ et $m (n - 1)$ . Voir par exemple le cours dispensé par Toulouse III : [1] pages 8 et 9. On peut se reporter aussi au livre classique de Scheffé (1959)

Test d'adéquation à la loi de Fisher

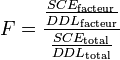
$F = \frac {\frac {SCE_\text{facteur}} {DDL_\text{facteur}}} {\frac {SCE_\text{total}} {DDL_\text{total}}}$

Il se trouve (comme on peut le voir dans la décomposition mathématique) que les deux termes sont tous les deux une estimation de la variabilité résiduelle si le facteur A n'a pas d'effet. De plus, ces deux termes suivent chacun une loi de χ², leur rapport suit donc une loi de F (voir plus loin pour les degrés de liberté de ces lois). Résumons :

Si le facteur A n'a pas d'effet, le rapport de $S a$ et $S r$ suit une loi de F et il est possible de vérifier si la valeur du rapport est « étonnante » pour une loi de F
Si le facteur A a un effet, le terme $S a$ n'est plus une estimation de la variabilité résiduelle et le rapport 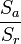$\frac{S_{a}}{S_{r}}$ ne suit plus une loi de F. On peut comparer la valeur du rapport à la valeur attendue pour une loi de F et voir, là aussi, à quel point le résultat est « étonnant ».

Résumer les choses ainsi permet de clarifier l'idée mais renverse la démarche : on obtient en pratique une valeur du rapport 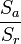$\frac{S_{a}}{S_{r}}$ qu'on compare à une loi de F, en se donnant un risque α (voir l'article sur les tests et leurs risques). Si la valeur obtenue est trop grande, on en déduit que le rapport ne suit vraisemblablement pas une loi de F et que le facteur A a un effet. On conclut donc à une différence des moyennes.

$C M B$ est l'estimateur $S A$ présenté au paragraphe précédent (première approche technique) et $C M W$ l'estimateur $S B$ . On en déduit le F de Fisher, dont la distribution est connue et tabulée sous les hypothèses suivantes :

Les résidus $ε$ sont distribués normalement
Avec une espérance nulle
Avec une variance $σ 2$ indépendante de la catégorie i
Avec une covariance nulle deux à deux (indépendance)

Le respect de ces hypothèses assure la validité du test d'analyse de la variance. On les vérifie a posteriori par diverses méthodes (tests de normalité, examen visuel de l'histogramme des résidus, examen du graphique des résidus en fonction des estimées) voir condition d'utilisation ci-dessous.

Exemple illustratif

Prenons un exemple pour illustrer la méthode. Imaginons un agriculteur qui souhaite acheter de nouvelles vaches pour sa production laitière. Il possède trois races différentes de vaches et se pose donc de la question de savoir si la race est importante pour son choix. Il possède comme informations la race de chacune de ses bêtes (c'est la variable explicative discrète ou facteur de variabilité, qui peut prendre 3 valeurs différentes) et leurs productions de lait journalières (c'est la variable à expliquer continue, qui correspond au volume de lait en litre).

Dans notre exemple, l'hypothèse nulle revient à considérer que toutes les vaches produisent la même quantité de lait journalière (au facteur aléatoire près) quelle que soit la race. L'hypothèse alternative revient à considérer qu'une des races produit significativement plus ou moins de lait que les autres.

Supposerons que les productions sont :

Pour la race A : 20,1 ; 19,8 ; 21,3 et 20,7
Pour la race B : 22,6 ; 24,1 ; 23,8 ; 22,5 ; 23,4 ; 24,5 et 22,9
Pour la race C : 31,2 ; 31,6 ; 31,0 ; 32,1 et 31,4

Analyse réalisée avec R :

> produc <- c(20.1, 19.8, 21.3, 20.7, 22.6, 24.1, 23.8, 22.5, 
23.4, 24.5, 22.9, 31.2, 31.6, 31.0, 32.1, 31.4)
> race <- as.factor(c("A", "A", "A", "A", "B", "B", "B", "B", "B", 
"B", "B", "C", "C", "C", "C", "C"))
# Regardons les moyennes par groupe:
> tapply(produc, race, mean)
A      B      C 
20.475 23.400 31.460 
# On remarque des différences entre groupes, mais sont-elles statistiquement significatives? 
Testons le par l'ANOVA:
> anova(lm(produc~race))
Analysis of variance Table

Response: produc
             Df     Sum Sq    Mean Sq    F value       Pr(>F)
race          2    307.918    153.959     357.44    4.338e-12 ***
Residuals    13      5.600      0.431                      
---
Signif. codes:    0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Les résultats de l'analyse sont présentés dans un tableau (les couleurs ont été ajouté pour faciliter l'explication). Le tableau contient 3 lignes : la première contient les titres des colonnes, la dernière contient l'analyse des résidus. La tableau contient également une ligne par facteur de variabilité (une seul dans cet exemple).

La première colonne (en rouge) indique les facteurs analysés : le facteur "race" et les résidus ("Residuals" (en)).
La seconde colonne (en bleu) indique le nombre de degrés de liberté : 3 races différentes - 1 = 2 degrés de libertés pour le facteur "race" ; 16 individus dans l'étude - 3 niveaux pour le facteur "race" = 13 degrés de liberté pour les résidus.
La cinquième colonne (en vert) indique le $F$ calculé dans cet exemple.
La sixième colonne (en marron) indique la probabilité que l'hypothèse nulle soit vraie (p-value). Dans cet exemple, la valeur très basse indique que l'on peut rejeter l'hypothèse nulle avec très peu de risque : l'agriculteur peut conclure "les 3 races de vaches ne produisent pas la même quantité journalière de lait". Le nombre d'étoiles à côté de la valeur de $p$ indique la confiance que l'on peut accorder au résultat : 3 étoiles indiquent que le résultat est très sûr.

Analyse de la variance à deux facteurs

Également appelé two-way ANOVA (en), l'analyse de la variance à deux facteurs s'applique lorsque l'on souhaite prendre en compte deux facteurs de variabilité.

Décomposition de la variance

Soit un premier facteur de variabilité pouvant prendre les niveaux $i = 1.. p$ , un second facteur de variabilité pouvant prendre les niveaux $j = 1.. q$ , $n i j$ le nombre d'individu dans le niveau $i$ du premier facteur et le niveau $j$ du second facteur et $n$ le nombre d'individu total. La variable à expliquer s'écrit $y i j k$ avec $i = 1.. p$ , $j = 1.. n i$ et $k = 1.. m j$ .

La variable à expliquer peut être modélisée par la relation :

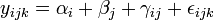
$y_{ijk} = \alpha_i + \beta_j + \gamma_{ij} + \epsilon_{ijk} ~$

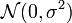avec $α i$ l'effet du niveau $i$ du premier facteur, $β j$ l'effet du niveau $j$ du second facteur, $γ i j$ l'effet d'interaction entre les deux facteurs et $ε i j k$ l'erreur aléatoire (qui suit alors une loi normale $\mathcal{N}(0, \sigma^2)~$ ).

Le calcul présenté dans le cas à un facteur peut être transposé au cas à deux facteurs :

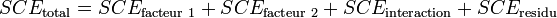
$SCE_\text{total} = SCE_\text{facteur 1} + SCE_\text{facteur 2} + SCE_\text{interaction} + SCE_\text{residu}~$

La part de la variance totale expliquée par le premier facteur ( $S C E facteur 1$ ), la part de la variance totale expliquée par le second facteur ( $S C E facteur 2$ ), l'interaction entre les deux facteurs ( $S C E interaction$ ) et la part de la variance totale qui ne peut être expliquée par le modèle ( $S C E residu$ , appelé aussi variabilité aléatoire ou bruit) sont données par les formules :

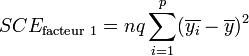
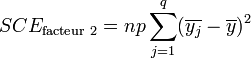
$SCE_\text{facteur 1} = nq \sum_{i=1}^p (\overline{y_i} - \overline{y})^2$	$SCE_\text{facteur 2} = np \sum_{j=1}^q (\overline{y_j} - \overline{y})^2$
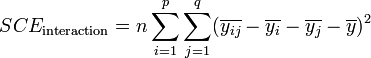
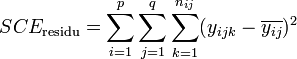
$SCE_\text{interaction} = n \sum_{i=1}^p \sum_{j=1}^q (\overline{y_{ij}} - \overline{y_i} - \overline{y_j} - \overline{y})^2$	$SCE_\text{residu} = \sum_{i=1}^p \sum_{j=1}^q \sum_{k=1}^{n_{ij}} (y_{ijk} - \overline{y_{ij}})^2$

L'analyse de l'interaction entre facteurs est relativement complexe^[1]. Dans le cas où les facteurs sont indépendants, on peut s'intéresser qu'aux effet principaux des facteurs. La formule devient alors :

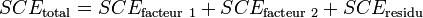
$SCE_\text{total} = SCE_\text{facteur 1} + SCE_\text{facteur 2} + SCE_\text{residu} ~$

Exemple illustratif

Notre exploitant laitier souhaite améliorer la puissance de son analyse en augmentant la taille de son étude. Pour cela, il inclut les données provenant d'une autre exploitation. Les chiffres qui lui sont fournit sont les suivant :

Pour la race A : 22,8 ; 21,7 ; 23,3 ; 23,1 ; 24,1 ; 22,3 et 22,7
Pour la race B : 23,1 ; 22,9 ; 21,9 ; 23,4 et 23,0
Pour la race C : 31,7 ; 33,1 ; 32,5 ; 35,1 ; 32,2 et 32,6

Analyse réalisée avec R :

> produc <- c(20.1, 19.8, 21.3, 20.7, 22.6, 24.1, 23.8, 22.5, 23.4, 
24.5, 22.9, 31.2, 31.6, 31.0, 32.1, 31.4, 22.8, 21.7, 23.3, 23.1, 
24.1, 22.3, 22.7, 23.1, 22.9, 21.9, 23.4, 23.0, 31.7, 33.1, 32.5, 
35.1, 32.2, 32.6)

> race <- as.factor(c("A", "A", "A", "A", "B", "B", "B", "B", "B", 
"B", "B", "C", "C", "C", "C", "C", "A", "A", "A", "A", "A", "A", 
"A", "B", "B", "B", "B", "B", "C", "C", "C", "C", "C", "C"))

> centre <- as.factor(c(rep("premier", 16), rep("second", 18)))

> anova(lm(produc~race*centre))
Analysis of variance Table

Response: produc
               Df    Sum Sq    Mean Sq     F value       Pr(>F)    
race            2    696.48     348.24    559.6811    < 2.2e-16 ***
centre          1      8.46       8.46     13.6012    0.0009636 ***
race:centre     2     12.23       6.11      9.8267    0.0005847 ***
Residuals      28     17.42       0.62                       
---
Signif. codes:    0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Analyse de la variance multifactorielle

Décomposition de la variance

On peut encore décomposer la variance en ajoutant un terme pour chaque facteur et un terme pour chaque interaction possible :

y_i = μ +	∑	α_j +	∑	γ_jk + ε_i
	j		j,k

avec $α j$ l'effet du j^ème facteur et $γ j k$ l'interaction entre le j^ème et le k^ème facteur.

L'analyse de la variance dans le cas de plusieurs facteurs de variabilité est relativement complexe : il est nécessaire de définir un modèle théorique correct, étudier les interactions entre les facteurs, analyser la covariance^[1].

Limites d'utilisation de l'analyse de la variance

Normalité des distributions

La décomposition de la variance est toujours valable, quelle que soit la distribution des variables étudiées. Cependant, lorsqu'on réalise le test de Fisher, on fait l'hypothèse de la normalité de ces distributions. Si les distributions s'écartent légèrement de la normalité, l'analyse de la variance est assez robuste pour être utilisée. 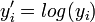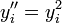Dans le cas où les distributions s'écartent fortement de la normalité, on pourra effectuer un changement de variables (par exemple, en prenant les variables $y'_i = log(y_i)~$ ou $y''_i = y_i^2$ ) ou utiliser un équivalent non paramétrique de l'analyse de la variance.

Article détaillé : Tests de normalité.

Homoscédasticité

A l'opposé, l'ANOVA fait une autre hypothèse très forte et moins évidente. Il est en effet nécessaire que la variance dans les différents groupes soit la même. C'est l'hypothèse d'homoscedasticité. L'ANOVA y est très sensible. Il est donc nécessaire de la tester avant toute utilisation.

Contrairement à ce que le nom de cette méthode laisse penser, celle-ci ne permet pas d'analyser la variance de la variable à expliquer mais de comparer les moyennes des distributions de la variable à expliquer en fonction des variables explicatives.

Approches non paramétriques

Lorsque les pré-supposés de l'ANOVA ne sont pas respectés (homoscédasticité par exemple), on entend souvent dire qu'il peut être plus judicieux d'utiliser l'équivalent non-paramétrique de l'ANOVA: le test de Kruskal Wallis pour le cas à un facteur ou, pour le cas à deux facteurs sans répétition, le test de Friedman. Pourtant, ces tests ne regardent pas la même chose. Comme il est écrit plus haut, l'ANOVA permet de comparer une mesure univariée entre des échantillons d'au moins deux populations statistiques. Le test de Kruskal-Wallis a pour hypothèse nulle l'homogénéité stochastique, c'est-à-dire que chaque population statistique est égale stochastiquement (on peut dire 'aléatoirement' pour simplifier) à une combinaison des autres populations. Ce test s'intéresse donc à la distribution contrairement à l'ANOVA et ne peut donc pas être considéré comme un équivalent au sens strict.

Voir aussi

Test (statistique)

Sources

SCHERRER, B. (1984). Comparaison des moyennes de plusieurs échantillons indépendants. Tiré de "Biostatistiques". Gaëtan Morin Éditeur. p. 422–463.
RUXTON, G.D. & BEAUCHAMP, G. (2008). Some suggestions about appropriate use of the Kruskal-Wallis test. Animal Behaviour 76, 1083-1087.

Références

↑ ^{a et b} Voir par exemple : Cours et TD de statistique de Lyon 1 pour un exemple d'analyse d'interaction dans un modèle à deux facteurs.

Portail des probabilités et des statistiques

Ce document provient de « Analyse de la variance ».

Catégorie : Statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Anova de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

ANOVA — abreviatura de análisis de la varianza Diccionario ilustrado de Términos Médicos.. Alvaro Galiano. 2010. ANOVA Abreviatura de análisis de la varianza. Diccionario Mosby Medicina, Enfermería y … Diccionario médico
ANOVA — Analyse de la variance L analyse de la variance (terme souvent abrégé par le terme anglais ANOVA : ANalysis Of VAriance) est un test statistique permettant de vérifier que plusieurs échantillons sont issus d une même population. Ce test s… … Wikipédia en Français
ANOVA — Als Varianzanalyse bezeichnet man eine große Gruppe datenanalytischer und mustererkennender statistischer Verfahren, die zahlreiche unterschiedliche Anwendungen zulassen. Ihnen gemeinsam ist, dass sie Varianzen und Prüfgrößen berechnen, um… … Deutsch Wikipedia
ANOVA — Analysis of variance A*nal y*sis of variance, n. (Statistics) a statistical technique by which the results of an observation or experiment are analyzed to determine the relative contributions of the different possible causative factors or… … The Collaborative International Dictionary of English
ANOVA Gauge R&R — (or ANOVA Gauge Repeatability Reproducibility) is a Measurement Systems Analysis technique which uses Analysis of Variance (ANOVA) random effects model to assess a measurement system. The evaluation of a measurement system is not limited to… … Wikipedia
Anova Books — is a UK based publishing company founded in 2005, with the acquisition of the Chrysalis Books Group from the Chrysalis Group. Since its inception, the firm has acquired or created several other imprints. Current imprints include: Batsford, a 150… … Wikipedia
Anova Hotel & Spa — (Монженевр,Франция) Категория отеля: Адрес: Hameau de l Obelisque, 05100 Монженевр, Франц … Каталог отелей
Anova Books — Год основания 2005 Расположение … Википедия
ANOVA-simultaneous component analysis — ASCA, ANOVA SCA, or analysis of variance – simultaneous component analysis is a method that partitions variation and enables interpretation of these partitions by SCA, a method that is similar to PCA. This method is a multi or even megavariate… … Wikipedia
ANOVA — abbreviation analysis of variance … New Collegiate Dictionary

Dictionnaires et Encyclopédies sur 'Academic'

Anova

Analyse de la variance

Sommaire

Principe

Décomposition de la variance

Test de Fisher

Remarques

Analyse de la variance à un facteur

Décomposition de la variance

Analyse des résidus

Test de Fisher

Exemple illustratif

Analyse de la variance à deux facteurs

Décomposition de la variance

Exemple illustratif

Analyse de la variance multifactorielle

Décomposition de la variance

Limites d'utilisation de l'analyse de la variance

Voir aussi

Sources

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Anova

Analyse de la variance

Sommaire

Principe

Décomposition de la variance

Test de Fisher

Remarques

Analyse de la variance à un facteur

Décomposition de la variance

Analyse des résidus

Test de Fisher

Exemple illustratif

Analyse de la variance à deux facteurs

Décomposition de la variance

Exemple illustratif

Analyse de la variance multifactorielle

Décomposition de la variance

Limites d'utilisation de l'analyse de la variance

Voir aussi

Sources

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link