- Lois de Snell-Descartes
-
Les lois de Snell-Descartes décrivent le comportement de la lumière à l'interface de deux milieux. Ces lois sont au nombre de deux, une pour la réflexion et une pour la réfraction. Avec la propagation rectiligne de la lumière dans les milieux homogènes et isotropes, ces lois sont à la base de l'optique géométrique.
Sommaire
Historique
Reproduction d'un manuscrit de Ibn Sahl contenant sa découverte des lois de la réfraction.
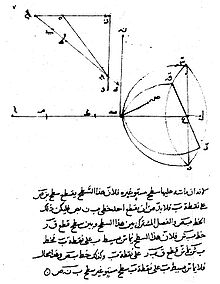
La loi de la réfraction est connue de Ibn Sahl (c. 940-1000)[1], en 983. En particulier, il calcule la "lentille anaclastique parfaite". Plus tard, la théorie de l'arc-en-ciel est connue dans le monde arabe (Al Farisi[2]).
Ensuite, en Europe, à la suite de la traduction latine du traité d'optique, l'optique se répand : Oxford (Robert Grossetête, Roger Bacon), Paris, Prague. La loi des petits angles est connue : Witelo (dit Vitellion) aurait repris les tables expérimentales de déviation établies par Ptolémée, mais c'est ensuite Kepler qui, dans les Paralipomènes à Vitellion, a énoncé explicitement la relation entre les (petits) angles d'incidence et de réfraction. Thomas Harriot est crédité d'avoir dressé des tables via la loi des sinus (1601) et d'expliquer l'arc-en-ciel (1606) ; mais il ne publie pas.
- Snell développe ses travaux, en même temps qu'il publie sa table des sinus (1621).
- Descartes publiera, en 1637, la loi dans son traité de Dioptrique (en annexe du Discours de la Méthode) .
- Les lois de Snell-Descartes peuvent être entièrement déduites du principe de Fermat, et en physique moderne des équations de Maxwell de l'électromagnétisme.
En Europe occidentale, la querelle de priorité - Snell ou Descartes ? - fut abondamment débattue ; compte-tenu de Ibn Sahl, Harriot, Kepler, c'est une « ancienne » querelle (voir controverses du cartésianisme, dioptrique).
L'ancienne querelleEn Europe occidentale, l'énoncé de la loi des sinus est attribuée à la fois à Descartes et à Snell, et ce fait sera l'objet d'une querelle de priorité si fréquente à cette époque ( début du XVIIe) : la polémique portant sur la question de savoir si Descartes a lui-même découvert cette loi ou simplement eu connaissance de celle établie peu de temps auparavant par Snell, ce dernier étant décédé sans l’avoir publiée. Si Leibniz et Huygens considéraient qu’en effet Descartes ne pouvait pas avoir été sans connaître la loi énoncée par Snell, les avis des historiens ne sont pas si tranchés. B. Maitte[3] évoque la connaissance que Descartes aurait eue du manuscrit de Snell non publié (qui, selon J.-P. Maury[4], aurait été confié à Rivet, professeur de théologie en relation avec le Père Mersenne[5], lui-même correspondant beaucoup avec Descartes). Mais selon P. Costabel[6] il n’y a aucune preuve en l’état actuel de la documentation historique quant au fait que Descartes ait eu communication du résultat de Snell. D’autres auteurs évoquent l’antériorité de Harriot qui aurait trouvé ladite loi mais n’aurait fourni à Kepler que les tables des mesures sans l’interprétation.
Les documents historiques actuellement retrouvés ne permettent pas de connaître la démarche de Snell. Pour ce qui concerne Descartes, quelques indications conduisent à considérer que l’idée des sinus fut directement liée à la recherche de la forme d’une lentille dite "parfaite", c’est-à-dire capable de faire converger exactement en un point un faisceau de rayons parallèles. Le profil pressenti du dioptre était celui d’une hyperbole et c’est l’étude géométrique de ce profil – qualifié d’anaclastique – qui a conforté Descartes dans le bien-fondé d’une loi en sinus : la conviction, pour ne pas dire la preuve, a résulté d’un ensemble de considérations, expérimentales (fabrication à la limite du possible d’une telle lentille par Ferrier) et théoriques (démonstration que la forme hyperbolique correspondait bien à une relation entre les sinus des angles par le géomètre Mydorge et par le mathématicien Beeckman). Ajoutons ici que cette préoccupation est née de l’invention de la lunette, lunette améliorée par Galilée et transmise à Kepler qui en a donné une première explication.
Loi de Snell-Descartes pour la réflexion
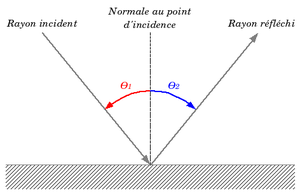
Schéma de principe de la loi de la réflexion : les faisceaux incidents et réfléchis forment avec la normale le même angle, qu'il faut orienter correctement.Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfléchissante, il est dit réfléchi après.
Le point de rencontre du rayon incident et de la surface réfléchissante est appelé point d'incidence.
La droite orthogonale à la surface réfléchissante au point d'incidence est appelée normale (à la surface réfléchissante).
Le plan contenant le rayon incident et la normale à la surface réfléchissante au point d'incidence est dit plan d'incidence.
L'angle orienté θ1 pris entre la normale au point d'incidence et le rayon incident est dit angle d'incidence.
L'angle orienté θ2 pris entre la normale au point d'incidence et le rayon réfléchi est dit angle de réflexion.
Les angles θ1 et θ2 sont positifs si orientés dans le sens trigonométrique, négatifs sinon. Attention : certains auteurs utilisent d'autres conventions.
La loi de la réflexion s'énonce ainsi :
-
- le rayon réfléchi est dans le plan d'incidence
- les angles incidents et réfléchis sont égaux en valeurs absolues ; θ1 et θ2 vérifient :
Loi de Snell-Descartes pour la réfraction
Schéma de la réfraction : le faisceau incident va être dévié selon la loi dite de Snell-Descartes.
Au-delà d'une certaine inclinaison, les rayons ne franchissent plus le dioptre : ils sont réfléchis.La loi de Snell-Descartes de la réfraction exprime le changement de direction d'un faisceau lumineux lors de la traversée d'une paroi, séparant deux milieux différents. Chaque milieu est caractérisé par sa capacité à « ralentir » la lumière, modélisée par son indice de réfraction n qui s'exprime sous la forme :
où v est la vitesse de la lumière dans ce milieu et c est la vitesse de la lumière dans le vide.
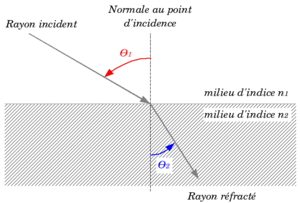
Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfractante (appelée dioptre), il est dit réfracté après.
Le point de rencontre du rayon incident et du dioptre est appelé point d'incidence.
Le plan contenant le rayon incident et la normale au dioptre, au point d'incidence est dit plan d'incidence.
L'angle orienté θ1 pris entre la normale au point d'incidence et le rayon incident est dit angle d'incidence.
L'angle orienté θ2 pris entre la normale au point d'incidence et le rayon réfracté est dit angle de réfraction.
Les angles θ1 et θ2 sont positifs si orientés dans le sens trigonométrique, négatifs sinon.
Soit n1 l'indice de réfraction du milieu dans lequel se propage le rayon incident et n2 celui du milieu dans lequel se propage le rayon réfracté.
La loi de la réfraction s'énonce ainsi :
-
- le rayon réfracté est dans le plan d'incidence
- la relation liant les indices de réfraction n1 et n2 de chacun des milieux et les angles incident θ1 et réfracté θ2 sont liés par la relation dite de Snell-Descartes :
Pour n1>n2 (et respectivement n1<n2) le rayon réfracté(ou incident) se rapproche plus rapidement du dioptre que le rayon incident(ou réfracté).Quand le rayon réfracté (ou incident) se retrouve mathématiquement sur le dioptre (sa limite) il y a alors réflexion totale.
Les lois empiriques de la réflexion et de la réfraction peuvent être interprétées par différents modèles : modèle ondulatoire de Huygens (principe de Huygens), modèle de moindre action de Fermat (principe de Fermat), modèle de l'onde électromagnétique de Maxwell.
Les lois de Snell-Descartes sont également utilisées dans la réflexion des ultrasons.
Forme vectorielle des lois de Snell-Descartes
La forme vectorielle permet d'exprimer les vecteurs directeurs des rayons réfléchi et réfracté à partir du vecteur directeur du rayon incident. Le résultat est identique à celui des formes scalaires, mais sous forme de vecteurs au lieu d'angles.
Étant donné le vecteur directeur I du rayon incident (en provenance d'une source lumineuse et en direction du dioptre) et le vecteur normal n au plan incident, on a[7] :
Note :
doit être positif. Sinon, il faut utiliserLa réflexion totale a lieu quand le radicande de la formule de cos θ2 est négatif.
Bibliographie
Pour l'histoire de l'optique :
- BLAY M. Les figures de l’arc-en-ciel. Paris : Belin, Coll. Pour la science, 2005.
- RONCHI V. Histoire de la lumière, (Reimpr.), Paris : Ed. Jacques Gabay, 1996.
Notes et références
- (en) A. Kwan, J. M. Dudley, E. Lantz, "Who really discovered Snell's law?", Physics World 15 (2002): 64-84. et Roshdi Rashed, Geometry and Dioptrics in Classical Islam (London: al-Furqan, 2005), XIII-1178-VI p., ISBN 1 873992 99 8
- R Rashed, Le modèle de la sphère transparente et l'explication de l'arc-en-ciel : Ibn al-Haytham - al-Farisi, Revue d'histoire des sciences 22 (1970), 109-140.
- MAITTE B. Histoire de l’arc-en-ciel. Paris : Seuil, Science ouverte, 2005
- MAURY J.-P. À l’origine de la recherche scientifique : Mersenne. Paris : Vuibert, 2003
- ROCHOT B. La correspondance scientifique du père Mersenne. Paris : Palais de la Découverte, 1966.
- COSTABEL P. Démarches originales de Descartes savant. Paris : Vrin, 1982.
- (en) Andrew S. Glassner, An Introduction to Ray Tracing, Morgan Kaufmann, 1989 (ISBN 0122861604) [lire en ligne]
Articles connexes
Catégories :- Optique géométrique
- Loi en physique
Wikimedia Foundation. 2010.
