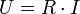Loi d'Ohm locale

Loi d'Ohm locale

Loi d'Ohm

Page d'aide sur l'homonymie Pour les articles homonymes, voir Ohm.

La loi d'Ohm est une loi physique permettant de relier l'intensité du courant électrique traversant un dipôle électrique à la tension à ses bornes. La loi d'Ohm a été nommée ainsi en l'honneur du physicien allemand Georg Ohm.

Sommaire

Point de vue macroscopique

En courant continu

La différence de potentiel ou tension U (en volts) aux bornes d'une résistance R (en ohms) est proportionnelle à l'intensité du courant électrique I (en ampères) qui la traverse.

Représentation schématique d'une résistance parcourue par un courant. La loi d'Ohm relie l'intensité i du courant à la valeur R de la résistance et à la tension U entre ses bornes par la relation U = R.I
U = R \cdot I \,

On peut en déduire :

  • I = \frac U R si R est non nul
  • R = \frac U I si I est non nul

La résistance s'exprime en ohms (symbole : Ω).

Cette loi porte le nom de Georg Ohm qui a travaillé sur le comportement des conducteurs métalliques. Elle s'applique de manière satisfaisante aux conducteurs métalliques thermostatés, c'est-à-dire maintenus à une température constante. Lorsque la température change, la valeur de la résistance change également de manière plus ou moins simple, ce qui impose d'introduire des termes correctifs. Par convention, on conserve la loi et on introduit les termes correctifs dans la valeur de la résistance du conducteur.

En courant alternatif

La loi précédente se généralise au cas des courants sinusoïdaux en utilisant les notations complexes. On note \underline{U}, \underline{I} la tension et le courant complexes. La loi d'Ohm s'écrit alors :

\underline{U}=\underline{Z} \cdot \underline{I}

Avec \underline{Z}\, : impédance complexe du dipôle considéré, qui peut être constitué de dipôles linéaires (résistances, condensateurs et inductances).

Point de vue local (mésoscopique)

Énoncé de la loi d'Ohm locale

D'un point de vue local, c'est-à-dire mésoscopique, la loi (locale) d'Ohm s'énonce en disant que la mobilité des porteurs de charge est indépendante de ||\vec{E}|| .

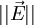Si on note 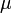\mu\, la mobilité des porteurs de charge, leur vitesse s'écrit alors 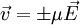\vec{v}=\pm \mu\vec{E} (la direction du mouvement dépend du signe des porteurs) ; la densité de courant 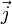\vec{j} associée à une densité de porteurs n\, vaut quant à elle :

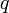\vec{j}=qn\vec{v}=qn\mu\vec{E} , où q\, est la charge électrique du porteur (en valeur absolue).

On note \sigma = qn\mu\, la conductivité électrique du matériau (pour un seul type de porteur).

On a alors la loi locale d'Ohm pour un seul type de porteur :

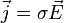\vec{j}=\sigma \vec{E} .

Si on a plusieurs types de porteurs, comme par exemple les électrons et les trous dans un semi-conducteur ou des ions différents dans un électrolyte, la densité de courant devient :

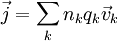\vec{j}= \sum_k n_k q_k \vec{v}_k ,

avec \vec{v}_k=\mu_k \vec{E} ,

donc \vec{j}= \left [\sum_k n_k q_k \mu_k \right ] \vec{E} .

On a alors la conductivité totale :

\sigma= \sum_k n_k q_k \mu_k \,

Voir aussi Loi de Nernst-Einstein.

Rapport avec la loi d'Ohm macroscopique : définition de la résistance

Considérons une portion de conducteur d'un point A à un point B et de section droite S, on a alors la différence de potentiel qui vaut :

V_A-V_B = \int_{A}^{B} \vec{E} \cdot d\vec{l}

et l'intensité :

i=\iint_S \vec{j} \cdot d\vec{S} = \iint_S \sigma \vec{E} \cdot d\vec{S} = \sigma \iint_S \vec{E} \cdot d\vec{S}

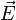Multiplions par une constante la différence de potentiel V_A-V_B\, , alors les conditions aux limites sont inchangées ainsi que les lignes de champ de \vec{E} , et l'expression \iint_S \vec{E} \cdot d\vec{S} est multipliée par la même constante, par conséquent le rapport :

\frac{V_A-V_B}{i} est indépendant de cette constante, c'est une "constante" (il dépend quand même de divers paramètres telle la température) appelée résistance électrique et notée R\,.
R=\frac{V_A-V_B}{i}=\frac{\int_{A}^{B} \vec{E}.d\vec{l}}{\sigma \iint_S \vec{E} \cdot d\vec{S}}

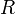Cette formule permet de calculer la résistance de diverses géométries de matériaux (filiforme, cylindrique, sphérique, ...).

Voir aussi


Liens externes

  • Portail de la physique Portail de la physique
  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
Ce document provient de « Loi d%27Ohm#.C3.89nonc.C3.A9 de la loi d.27Ohm locale ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi d'Ohm locale de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Loi d'Ohm — Pour les articles homonymes, voir Ohm. La loi d Ohm est une loi physique permettant de relier l intensité du courant électrique traversant un dipôle électrique à la tension à ses bornes (elle permet de déterminer la valeur d une résistance). La… …   Wikipédia en Français

  • Loi de Joule (électricité) — Effet Joule L effet Joule est la manifestation thermique de la résistance électrique. Il se produit lors du passage d un courant électrique dans tout matériau conducteur présentant une résistance, à l exception des supraconducteurs qui… …   Wikipédia en Français

  • Conducteur en équilibre électrostatique — Un conducteur électrique en équilibre électrostatique est un conducteur qui n est parcouru par aucun courant. Cela signifie que toutes les charges électriques libres internes au conducteur sont toutes immobiles . Dans n importe quel conducteur,… …   Wikipédia en Français

  • Conducteur En Équilibre Électrostatique — Un conducteur électrique en équilibre électrostatique est un conducteur pour lequel les charges libres sont en moyenne fixes, par conséquent il y a absence de courant à l intérieur de celui ci. Supposons ce conducteur ohmique i.e. qu il vérifie… …   Wikipédia en Français

  • Conducteur en equilibre electrostatique — Conducteur en équilibre électrostatique Un conducteur électrique en équilibre électrostatique est un conducteur pour lequel les charges libres sont en moyenne fixes, par conséquent il y a absence de courant à l intérieur de celui ci. Supposons ce …   Wikipédia en Français

  • Densite de courant — Densité de courant Pour les articles homonymes, voir densité (homonymie). La densité de courant est un objet qui décrit le courant électrique qui circule à l échelle locale, en un point d un matériau. Mathématiquement, il s agit d un champ de… …   Wikipédia en Français

  • Densité De Courant — Pour les articles homonymes, voir densité (homonymie). La densité de courant est un objet qui décrit le courant électrique qui circule à l échelle locale, en un point d un matériau. Mathématiquement, il s agit d un champ de vecteurs qui associe à …   Wikipédia en Français

  • Densité de courant — Pour les articles homonymes, voir densité (homonymie). La densité de courant décrit le courant électrique qui circule à l échelle locale, en un point d un matériau. Mathématiquement, il s agit d un champ de vecteurs qui associe à tout point de l… …   Wikipédia en Français

  • Vecteur densite de courant — Densité de courant Pour les articles homonymes, voir densité (homonymie). La densité de courant est un objet qui décrit le courant électrique qui circule à l échelle locale, en un point d un matériau. Mathématiquement, il s agit d un champ de… …   Wikipédia en Français

  • Vecteur densité de courant — Densité de courant Pour les articles homonymes, voir densité (homonymie). La densité de courant est un objet qui décrit le courant électrique qui circule à l échelle locale, en un point d un matériau. Mathématiquement, il s agit d un champ de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”