- Loi d'Amdahl
-
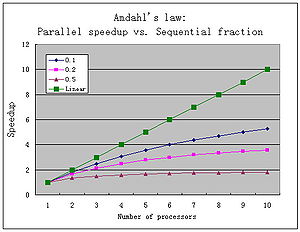
Évolution du gain en vitesse d'exécution d'un programme en fonction du nombre de processeurs pour différentes valeurs de 1-s selon la Loi d'Amdahl
La loi d'Amdahl, énoncée par Gene Amdahl, exprime le gain de performance qu'on peut attendre d'un ordinateur en améliorant une composante de sa performance. Sous sa forme générale elle indique que le gain de performance égale le temps d'exécution d'une tâche complète sans l'amélioration divisé par le temps d'exécution de la même tâche avec l'amélioration.
Dans sa version originale, la loi d'Amdahl s'articule sur une simple règle de trois. Elle indique le gain de temps que va apporter un système multiprocesseur en fonction :
- du nombre de processeurs N
- de la proportion d'activité parallélisable s
le tout en négligeant à ce stade le surcroit d'activité lié à la gestion du parallélisme lui-même. La loi a la forme :
Avec N tendant vers l'infini, on obtient :
.Ce que montre la loi d'Amdahl, c'est que la fraction du temps d'exécution qui peut tirer profit de l'amélioration limite le gain de performance global, quelle que soit la valeur de l'amélioration de la composante.
Sommaire
Un rendement parfois décevant
- Certaines applications comme le traitement d'image tirent un très bon parti du parallélisme. s, dans leur cas, peut se retrouver voisin de 0,95.
- D'autres comme l'analyse numérique pourront tirer profit d'un changement d'algorithme (par exemple le remplacement d'une Méthode de Gauss-Seidel par une Méthode de Jacobi qui converge plus lentement, mais est totalement parallélisable).
Les autres cas se montrent décevants : pour s= 0,5, le passage à un biprocesseur fait gagner 25% de temps. Le passage à 12 processeurs fait passer ce gain de temps à 45,83%.
Note : La loi d'Amdahl est considérée ici dans le cas d'un système où tous les processeurs sont consacrés au même utilisateur, et à des threads du même processus. Ce cas ne se rencontre pas toujours. Dans la pratique, les résultats seront bien plus mauvais encore si l'on ne gère pas l'affinité processeur (processor affinity) qui veille à ce que les mêmes processeurs reprennent dans la mesure du possible les mêmes processus, afin d'éviter des rechargements intempestifs de cache.
Un moyen de faire remonter s
Un cas où s se retrouve évidemment voisin de 1 est celui où les processeurs exécutent des tâches différentes : étant indépendantes, elles sont ipso facto parallélisables, et de surcroît sans le moindre effort à entreprendre pour assurer cette parallélisation. Les problèmes restent à ce stade que :
- Le temps écoulé pour une application donnée n'est pas directement réduit : une simulation de quatre heures continuera à faire attendre quatre heures ses résultats (mais sera moins ralentie par les autres processus si elle revendique qu'un processeur lui soit dédié en propre).
- L'antémémoire et le cache disque se retrouvent plus encombrés de données appartenant à des processus différents, et il faut prévoir leur augmentation de taille en conséquence. Le problème disparaît pour l'antémémoire lorsque celle-ci se trouve sur le microprocesseur lui-même, ce qui règle du même coup les effets d'échelle.
Une autre loi d'Amdahl
Une loi plus ancienne d'Amdahl concernait un équilibre observé empiriquement dans les ordinateurs : une instruction par seconde requiert un octet de mémoire et un bit/seconde de capacité d'entrée-sortie. De fait, cette loi semble être restée valable assez longtemps (100 MIPS, 100 Mo de RAM et 100 Mb/s s'observaient vers 2000 et les réseaux gigabit ont commencé à se répandre à peu près en même temps que les mémoires de 1 Go).
Voir aussi
Bibliographie
- Gene Amdahl, "Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities", AFIPS Conference Proceedings, (30), pp. 483-485, 1967.
- ISBN 1-55860-329-8, John L. Hennessy & David A. Paterson, Computer Architecture a Quantitative Approach, second edition, pp 29-32, 1996
- http://www.cs.wisc.edu/multifacet/papers/tr1593_amdahl_multicore.pdf
Wikimedia Foundation. 2010.
