Methode de Jacobi

Methode de Jacobi

Méthode de Jacobi

La méthode de Jacobi, due au mathématicien allemand Karl Jacobi, est une méthode itérative de résolution d'un système matriciel de la forme Ax=b. Pour cela, on utilise une suite x(k) qui converge vers un point fixe x, solution du système d'équations linéaires.

Sommaire

Principe de construction

On cherche à construire l'algorithme pour x(0) donné, la suite x(k + 1) = F(x(k)) avec k \in \N.

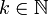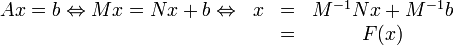
A = M − N où M est une matrice inversible. \begin{matrix} Ax=b \Leftrightarrow Mx=Nx+b \Leftrightarrow & x &=& M^{-1}Nx+M^{-1}b \\ & &=& F(x)\end{matrix}
où F est une fonction affine. M − 1N est alors appelée Matrice de Jacobi. Attention, l'algorithme qui suit n'est valable que si la matrice A est à diagonale strictement dominante sur les lignes.

Algorithme

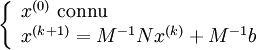
\left\{ \begin{array}{l} x^{(0)} \; \mbox{connu}\\ x^{(k+1)} = M^{-1}Nx^{(k)}+M^{-1}b \end{array} \right.


Si x est solution de Ax = b alors x = M − 1Nx + M − 1b .

Vecteur erreur

Soit e(k) le vecteur erreur

e(k + 1) = x(k + 1) − x(k) = M − 1N(x(k) − x(k − 1)) = M − 1Ne(k)
On pose B = M − 1N, ce qui donne e(k + 1) = Be(k) = B(k + 1)e(0).

Convergence

L'algorithme converge si 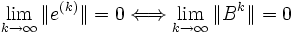\lim_{k \to \infty} \| e^{(k)} \| = 0 \Longleftrightarrow \lim_{k \to \infty} \| B^k \| = 0 (c-à-d. Bk tend vers la matrice nulle).



Théorème : Une condition nécessaire et suffisante pour que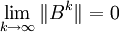 \lim_{k \to \infty} \| B^k \| = 0 est que le rayon spectral (plus grande valeur propre en module) de B soit strictement inférieur à 1.
Théorème : La méthode converge quel que soit x(0) pour les systèmes linéaires dont la matrice est à diagonale strictement dominante.

Méthode de Jacobi

On décompose la matrice A de la façon suivante : A = D-E-F avec D la diagonale, -E la partie en dessous de la diagonale et -F la partie au dessus. Dans la méthode de Jacobi, on choisit M = D et N = E+F (dans la méthode de Gauss-Seidel, M = D-E et N = F).

x(k + 1) = D − 1(E + F)x(k) + D − 1b

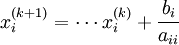x^{(k+1)}_i=\cdots x^{(k)}_i+\frac{b_i}{a_{ii}} avec
pour la ligne i de D − 1(E + F) :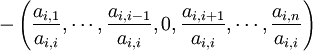 -\left(\frac{a_{i,1}}{a_{i,i}},\cdots, \frac{a_{i,i-1}}{a_{i,i}},0,\frac{a_{i,i+1}}{a_{i,i}},\cdots, \frac{a_{i,n}}{a_{i,i}}\right)


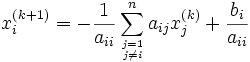
x^{(k+1)}_i= -\frac{1}{a_{ii}} \sum_{j=1 \atop j \ne i}^n a_{ij}x^{(k)}_j + \frac{b_i}{a_{ii}}

Vecteur résidu

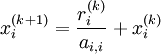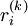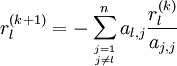Soit r(k) = De(k) le vecteur résidu. On peut écrire x_i^{(k+1)}=\frac{r_i^{(k)}}{a_{i,i}} + x_i^{(k)} avec r_i^{(k)} que l'on calcule de la manière suivante :r_l^{(k+1)}=-\sum_{j=1 \atop j \ne l}^n a_{l,j} \frac{r_l^{(k)}}{a_{j,j}}.

Test d'arrêt

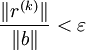
Pour le test d'arrêt, on utilise le vecteur résidu, ce qui donne, pour une précision donnée ε : \frac{\|r^{(k)} \|}{\|b\|} < \varepsilon

Conclusion

Cette méthode a un coût de l'ordre de 3n2 + 2n par itération. Elle converge moins vite que la méthode de Gauss-Seidel, mais est très facilement parallélisable.

Voir aussi

Articles connexes

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thode de Jacobi ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Methode de Jacobi de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Méthode De Jacobi — La méthode de Jacobi, due au mathématicien allemand Karl Jacobi, est une méthode itérative de résolution d un système matriciel de la forme Ax=b. Pour cela, on utilise une suite x(k) qui converge vers un point fixe x, solution du système d… …   Wikipédia en Français

  • Méthode de jacobi — La méthode de Jacobi, due au mathématicien allemand Karl Jacobi, est une méthode itérative de résolution d un système matriciel de la forme Ax=b. Pour cela, on utilise une suite x(k) qui converge vers un point fixe x, solution du système d… …   Wikipédia en Français

  • Méthode de Jacobi — La méthode de Jacobi, due au mathématicien allemand Karl Jacobi, est une méthode itérative de résolution d un système matriciel de la forme Ax=b. Pour cela, on utilise une suite x(k) qui converge vers un point fixe x, solution du système d… …   Wikipédia en Français

  • Methode iterative — Méthode itérative En analyse numérique, une méthode itérative résout un problème (comme une équation ou un système d équations) en utilisant une valeur initiale, puis en la raffinant par une succession d approximations se rapprochant… …   Wikipédia en Français

  • Méthode Itérative — En analyse numérique, une méthode itérative résout un problème (comme une équation ou un système d équations) en utilisant une valeur initiale, puis en la raffinant par une succession d approximations se rapprochant graduellement de la solution.… …   Wikipédia en Français

  • Methode de Gauss-Seidel — Méthode de Gauss Seidel La méthode de Gauss Seidel est une méthode itérative de résolution d un système matriciel de la forme Ax = b. Pour cela, on utilise une suite x(k) qui converge vers un point fixe x, solution du système d équations… …   Wikipédia en Français

  • Méthode De Gauss-Seidel — La méthode de Gauss Seidel est une méthode itérative de résolution d un système matriciel de la forme Ax = b. Pour cela, on utilise une suite x(k) qui converge vers un point fixe x, solution du système d équations linéaires. En notant A = [aij]ij …   Wikipédia en Français

  • Méthode de gauss-seidel — La méthode de Gauss Seidel est une méthode itérative de résolution d un système matriciel de la forme Ax = b. Pour cela, on utilise une suite x(k) qui converge vers un point fixe x, solution du système d équations linéaires. En notant A = [aij]ij …   Wikipédia en Français

  • Jacobi — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Jacobi est un nom de famille notamment porté par : Johann Georg Jacobi (1740 1814), poète allemand ; Friedrich Heinrich Jacobi (1743… …   Wikipédia en Français

  • Méthode de surrelaxation successive — En analyse numérique, la méthode de surrelaxation successive est une variante de la méthode de Gauss Seidel pour résoudre un système d équations linéaires. La convergence de cet algorithme est généralement plus rapide. Une approche similaire peut …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”