Diffie-Hellman

En cryptographie, l'échange de clés Diffie-Hellman, du nom de ses auteurs Whitfield Diffie et Martin Hellman, est une méthode par laquelle deux personnes nommées conventionnellement Alice et Bob peuvent se mettre d'accord sur un nombre (qu'ils peuvent utiliser comme clé pour chiffrer la conversation suivante) sans qu'une troisième personne appelée Ève puisse découvrir le nombre en écoutant.

Sommaire 1 Principe 2 Exemple 3 Fondement mathématique 4 L'attaque de l'Homme du milieu 4.1 Solution 5 Articles connexes

Principe

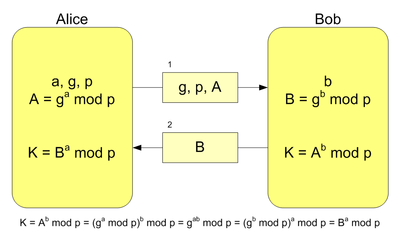
• Alice et Bob ont choisi un groupe (soit un corps fini, dont ils n'utilisent que la multiplication, soit une courbe elliptique) et une génératrice g de ce groupe.
• Alice choisit un nombre au hasard a, élève g à la puissance a, et dit à Bob g^a mod p.
• Bob fait de même avec le nombre b.
• Alice, en élevant le nombre reçu de Bob à la puissance a, obtient g^ba mod p.
• Bob fait le calcul analogue et obtient g^ab mod p, qui est le même. Mais puisqu'il est difficile d'inverser l'exponentiation dans un corps fini, c’est-à-dire de calculer le logarithme discret, Ève ne peut pas découvrir a et b, donc ne peut pas calculer g^ab mod p.

Exemple

Alice Secret Public Calcul p, g a ga mod p … (gb mod p)a mod p

=

Bob Calcul Public Secret p, g b … gb mod p (ga mod p)b mod p

1. Alice et Bob choisissent un nombre premier p et une base g. Dans notre exemple, p=23 et g=3
2. Alice choisit un nombre secret a=6
3. Elle envoie à Bob la valeur g^a mod p = 3⁶ mod 23 = 16
4. Bob choisit à son tour un nombre secret b=15
5. Bob envoie à Alice la valeur g^b mod p = 3¹⁵ mod 23 = 12
6. Alice peut maintenant calculer la clé secrète : (g^b mod p)^a mod p = 12⁶ mod 23 = 9
7. Bob fait de même et obtient la même clé qu'Alice : (g^a mod p)^b mod p = 16¹⁵ mod 23 = 9

Fondement mathématique

Le concept utilise la notion de groupe multiplicatif avec des entiers (modulo p) avec p un nombre premier. En gros, les opérations mathématiques (multiplication, puissance, division) sont utilisées telles quelles mais le résultat doit être divisé par p pour obtenir le reste (modulo). Les groupes ayant la propriété de l'association des puissances, l'égalite (g^b)^a = (g^a)^b est valide et les deux parties obtiennent bel et bien la même clé secrète.

La sécurité de ce protocole réside dans la difficulté du problème du logarithme discret : pour que Ève retrouve g^ab à partir de g^a et g^b, elle doit élever l'un ou l'autre à la puissance b ou à la puissance a respectivement. Mais déduire a (resp. b) grâce à g^a (resp. g^b) est un problème que l'on ne sait pas résoudre efficacement. Ève est donc dans l'impossibilité (calculatoire) de déduire g^ab.

Il faut toutefois que le groupe de départ soit bien choisi et que les nombres utilisés soient suffisamment grands pour éviter une attaque par recherche exhaustive. À l'heure actuelle, un nombre premier p de l'ordre de 300 chiffres ainsi que a et b de l'ordre de 100 chiffres sont tout simplement impossibles à casser même avec les meilleurs algorithmes de résolution du logarithme discret (source ?). Si une solution pratique pour résoudre un logarithme discret venait à apparaître, d'autres systèmes cryptographiques pourraient tomber, notamment ElGamal qui repose sur ce principe.

L'attaque de l'Homme du milieu

Ce protocole est vulnérable à l'attaque de l'homme du milieu qui implique un attaquant capable de lire et de modifier tous les messages échangés entre Alice et Bob. Cette attaque repose sur l'interception des nombres g^a et g^b ce qui est facile puisqu'ils sont échangés en clair ; l'élément g étant supposé connu par tous les attaquants.

Pour retrouver les nombres a et b et ainsi casser complètement l'échange, il faut calculer le logarithme discret des nombres g^a et g^b, ce qui est impossible en pratique. Mais dans l'attaque de l'homme du milieu, l'attaquant se place entre Alice et Bob, intercepte la clé g^a envoyé par Alice et envoie à Bob une autre clé g^a', se faisant passer pour Alice. De même, il remplace la clé g^b envoyée par Bob à Alice par une clé g^b', se faisant passer pour Bob. L'attaquant peut ainsi communiquer avec Alice en utilisant la clé partagée g^ab' et communiquer avec Bob en utilisant la clé partagée g^a'b.

Alice et Bob croient ainsi avoir échangé une clé secrète alors qu'en réalité ils ont chacun échangé une clé secrète avec l'attaquant, l'homme du milieu.

Solution

La parade classique à cette attaque consiste à signer les échanges de valeurs à l'aide d'une paire de clés asymétriques certifiées par une tierce partie fiable, ou dont les moitiés publiques ont été échangées auparavant par les deux participants.

Alice peut ainsi être assurée que la clé qu'elle reçoit provient effectivement de Bob, et inversement pour Bob.

Articles connexes

• Complexité algorithmique
• Cryptographie asymétrique
• Martin Hellman
• Whitfield Diffie
• Ralph Merkle
• Rivest Shamir Adleman (RSA)
• ElGamal
• Keyed-Hash Message Authentication Code (HMAC)

• Portail de la cryptologie
• Portail de la sécurité informatique