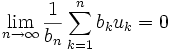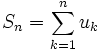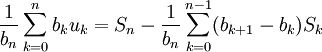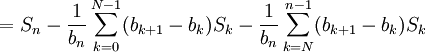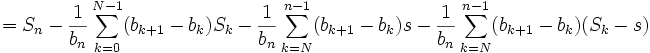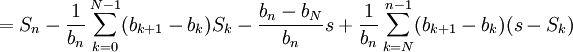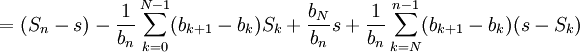Lemme de kronecker

Lemme de Kronecker

Le lemme de Kronecker est un résultat d'analyse concernant les séries de nombres réels.

Sa forme la plus connue est la forme suivante, utilisée en particulier en probabilités dans une preuve classique de la loi des grands nombres :

Si la série de terme général 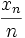$\frac{x_n}{n}$ converge alors 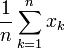$\frac1{n}\sum_{k=1}^n x_k$ tend vers 0 lorsque n tend vers l'infini.

Ce résultat admet une généralisation qui en rend la preuve assez naturelle:

Pour une série convergente de terme général $u n$ , et pour toute suite croissante de réels positifs $(b n)$ divergeant vers l'infini, on a :

$\lim_{n\rightarrow \infty} \frac{1}{b_n} \sum_{k=1}^n b_ku_k=0$

Preuve: On pose

$S_n=\sum_{k=1}^n u_k$

Une sommation d'Abel donne :

$\frac1{b_n}\sum_{k=0}^n b_k u_k = S_n - \frac1{b_n}\sum_{k=0}^{n-1}(b_{k+1} - b_k)S_k$

$=S_n - \frac1{b_n}\sum_{k=0}^{N-1}(b_{k+1} - b_k)S_k - \frac1{b_n}\sum_{k=N}^{n-1}(b_{k+1} - b_k)S_k$

$= S_n - \frac1{b_n}\sum_{k=0}^{N-1}(b_{k+1} - b_k)S_k - \frac1{b_n}\sum_{k=N}^{n-1}(b_{k+1} - b_k)s - \frac1{b_n}\sum_{k=N}^{n-1}(b_{k+1} - b_k)(S_k - s)$

$= S_n - \frac1{b_n}\sum_{k=0}^{N-1}(b_{k+1} - b_k)S_k - \frac{b_n-b_N}{b_n}s + \frac1{b_n}\sum_{k=N}^{n-1}(b_{k+1} - b_k)(s - S_k)$

$= (S_n - s) - \frac1{b_n}\sum_{k=0}^{N-1}(b_{k+1} - b_k)S_k + \frac{b_N}{b_n}s + \frac1{b_n}\sum_{k=N}^{n-1}(b_{k+1} - b_k)(s - S_k)$

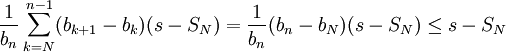Quand $n$ tend vers l'infini, le premier terme converge vers zéro car la suite $(S n)$ converge vers $s$ . Le deuxième et le troisième termes tendent vers 0 car $(b n)$ tend vers $+\infty$ . Le dernier terme est positif et majoré par $\frac1{b_n}\sum_{k=N}^{n-1}(b_{k+1} - b_k)(s - S_N)=\frac1{b_n}(b_{n} - b_N)(s - S_N)\le s-S_N$ . Par conséquent, la limite supérieure de la suite 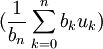$(\frac1{b_n}\sum_{k=0}^n b_k u_k )$ est majorée par $s - S N$ pour tout $N$ entier positif. En faisant tendre $N$ vers l'infini, on obtient le résultat énoncé.

Portail des mathématiques

Ce document provient de « Lemme de Kronecker ».

Catégories : Série | Lemme de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme de kronecker de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Lemme De Kronecker — Le lemme de Kronecker est un résultat d analyse concernant les séries de nombres réels. Sa forme la plus connue est la forme suivante, utilisée en particulier en probabilités dans une preuve classique de la loi des grands nombres : Si la… … Wikipédia en Français
Lemme de Kronecker — Le lemme de Kronecker est un résultat d analyse concernant les séries de nombres réels. Sa forme la plus connue est la forme suivante, utilisée en particulier en probabilités dans une preuve classique de la loi des grands nombres : Si la… … Wikipédia en Français
Kronecker — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Kronecker peut désigner Leopold Kronecker (1823 1891), un mathématicien et logicien allemand, et dont les articles suivants portent le nom :… … Wikipédia en Français
Lemme De Schur — En mathématiques et plus précisément en algèbre linéaire, le lemme de Schur est un lemme technique utilisé particulièrement dans la théorie de la représentation des groupes. Il a été démontré en 1907 par Issai Schur (1875 1941) dans le cadre de… … Wikipédia en Français
Lemme de schur — En mathématiques et plus précisément en algèbre linéaire, le lemme de Schur est un lemme technique utilisé particulièrement dans la théorie de la représentation des groupes. Il a été démontré en 1907 par Issai Schur (1875 1941) dans le cadre de… … Wikipédia en Français
Lemme de Schur — En mathématiques et plus précisément en algèbre linéaire, le lemme de Schur est un lemme technique utilisé particulièrement dans la théorie de la représentation des groupes. Il a été démontré en 1907 par Issai Schur dans le cadre de ses travaux… … Wikipédia en Français
Lemme de Milnor — Théorème de la boule chevelue Si un champ de vecteurs sur une sphère est symbolisé par des cheveux de longueur constante, le théorème de la boule chevelue stipule que la sphère contient au moins un épi. La figure en contient deux, un sur chaque… … Wikipédia en Français
Leopold Kronecker — Pour les articles homonymes, voir Kronecker. Leopold Kronecker Leopold Kronecker Naissance 7 décembre 1823 Legn … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Lemme de kronecker