- Lemme de könig
-
Lemme de König
Pour les articles homonymes, voir Théorème de König.Le lemme de König est un lemme de la théorie des graphes que l'on doit au mathématicien hongrois Dénes Kőnig. Il énonce que :
- Tout arbre infini à branchement fini a une branche infinie.
Sommaire
Définitions
Un arbre est un ensemble d'objets, appelés nœuds, tels qu'il y ait une relation binaire de succession immédiate et un nœud d'origine O qui satisfont aux conditions suivantes :
- O n'est le successeur immédiat d'aucun nœud.
- Tout nœud sauf O est le successeur immédiat d'un unique nœud.
- Tous les nœuds sont des successeurs de O.
Un nœud A est un successeur d'un autre D s'il existe une suite finie de nœuds qui commence par D, qui finit par A, et qui est telle que tout nœud est un successeur immédiat (au sens de la structure de l'arbre) de celui qui le précède dans la suite.
Un arbre est à branchement fini lorsque tous les nœuds n'ont qu'un nombre fini de successeurs immédiats.
Un arbre est infini lorsqu'il a un nombre infini de nœuds.
Une branche d'un arbre est une suite finie ou infinie de nœuds N(i), qui commence par O, et qui est telle que pour tout i, N(i+1) est un successeur immédiat de N(i).
Voir aussi arbre (mathématiques) pour une définition plus générale et plus puissante (arbres non-dénombrables).
Preuve
La preuve de Kőnig est brève.
Un nœud est dit infini s'il a un nombre infini de successeurs.
Supposons qu'on ait un arbre infini d'origine O à branchement fini.
O est infini. Comme O n'a qu'un nombre fini de successeurs immédiats, l'un d'entre eux au moins, noté N(1), est infini ; sinon O ne serait pas infini. De même l'un au moins, noté N(2), des successeurs immédiats de N(1) est infini. On définit ainsi un nombre infini de nœuds N(i), pour tout entier positif i, qui ensemble forment une branche infinie.
(Remarque: on utilise ici l'axiome des choix dépendants, forme faible de l'axiome du choix.)
Autre formulation
- Une relation acyclique à branchement fini est globalement finie si et seulement si tous les éléments sont accessibles.
Une relation
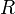sur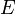 
est à branchement fini si pour tout 
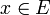l'ensemble 
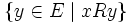est fini.Une relation
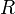est globablement finie si pour tout 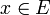l'ensemble 
est fini, où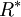 
est la fermeture réflexive et transitive de 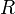.Une relation
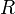est acyclique si 
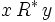et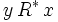 
implique 
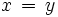.L'ensemble des éléments accessibles par
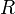est le plus petit ensemble tel que 
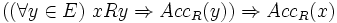.Cette formulation a l'avantage de ne pas faire référence à l'infini et de ne pas utiliser de négations inutiles.
Voir aussi
- Théorème de compacité.
- Théorème de complétude de Gödel.
- Raymond Smullyan, First-order logic.
Portail des mathématiques
Catégories : Logique mathématique | Théorème de mathématiques
Wikimedia Foundation. 2010.
