Lemme de borel
- Lemme de borel
-
Lemme de Borel
En mathématiques, le lemme de Borel est un résultat important concernant les équations aux dérivées partielles, portant le nom de celui qui l'a découvert: Émile Borel.
Supposons que U soit un ouvert dans un espace euclidien Rn, et supposons que f0,f1,... soit une séquence de fonctions continues et à valeurs complexes sur U. Alors il existe une fonction continue F = F(t,x) définie sur R×U à valeurs complexes , telle que:
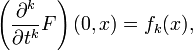
pour tout k = 0,1,..., et x dans U.
Une preuve constructiviste de ce résultat a été donnée par Golubitsky en 1974.
References
- M. Golubitsky, V. Guillemin (1974). Stable mappings and their singularities. Springer-Verlag, Graduate texts in Mathematics: Vol. 14. ISBN 0-387-90072-1.
 Portail des mathématiques
Portail des mathématiques
Catégories : Équation aux dérivées partielles | Lemme de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Lemme de borel de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Lemme De Borel — En mathématiques, le lemme de Borel est un résultat important concernant les équations aux dérivées partielles, portant le nom de celui qui l a découvert: Émile Borel. Supposons que U soit un ouvert dans un espace euclidien Rn, et supposons que… … Wikipédia en Français
Lemme de Borel — En mathématiques, le lemme de Borel est un résultat important concernant les équations aux dérivées partielles, portant le nom de celui qui l a découvert: Émile Borel. Supposons que U soit un ouvert dans un espace euclidien Rn, et supposons que… … Wikipédia en Français
Lemme de Borel-Cantelli — Théorème de Borel Cantelli Sommaire 1 Introduction 2 Limite supérieure d ensembles 3 Théorème de Borel Cantelli (théorie de la mesure) 4 … Wikipédia en Français
Lemme de Borel-Carathéodory — Ne doit pas être confondu avec Lemme de Borel Cantelli. En mathématiques, le lemme de Borel Carathéodory, nommé d après Émile Borel et Constantin Carathéodory, est un lemme estimant le maximum d une fonction analytique dans un disque centré … Wikipédia en Français
Lemme De Césaro — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français
Lemme de Cesaro — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français
Lemme de Césaro — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français
Lemme de césaro — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français
Lemme de Cousin — En mathématiques, le lemme de Cousin[1] est une propriété de la droite réelle équivalente à l existence de la borne supérieure pour les parties majorées de . Il joue un rôle important dans l intégrale de Kurzweil Henstock, mais permet également… … Wikipédia en Français
Lemme de Riesz — Pour les articles homonymes, voir Théorème de Riesz. Le lemme de Riesz, dû au mathématicien Frigyes Riesz, est un résultat d analyse fonctionnelle sur les sous espaces vectoriel fermés d un espace vectoriel normé réel. Sa principale conséquence… … Wikipédia en Français