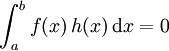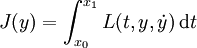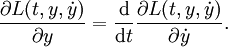Lemme Fondamental Du Calcul Des Variations
- Lemme Fondamental Du Calcul Des Variations
-
Lemme fondamental du calcul des variations
Le lemme fondamental du calcul des variations est un lemme essentiel au calcul des variations. Il énonce que si f est une fonction continue sur l'intervalle [a,b], et
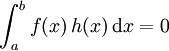
pour toute fonction ![h\in C^\infty [a,b]](/pictures/frwiki/102/fee43d4ace98a758497786f58013b0e7.png) avec h(a) = h(b) = 0, alors f(x) est identiquement nulle sur l'intervalle ouvert (a,b).
avec h(a) = h(b) = 0, alors f(x) est identiquement nulle sur l'intervalle ouvert (a,b).
Plus généralement, ce résultat de ce lemme reste vrai avec 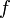 localement intégrable sur un ensemble ouvert U de
localement intégrable sur un ensemble ouvert U de 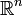 et les fonctions h sont de classe
et les fonctions h sont de classe 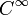 et à support compact dans U (La conclusion est changée par « f est nulle presque partout »).
et à support compact dans U (La conclusion est changée par « f est nulle presque partout »).
Applications
Ce lemme est utilisé pour prouver que les extrema de la fonctionnelle
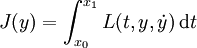
sont des solutions faibles de l'équation d'Euler-Lagrange:
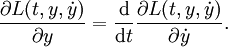
Références
 Portail des mathématiques
Portail des mathématiques
Catégories : Calcul des variations | Lemme de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Lemme Fondamental Du Calcul Des Variations de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Lemme fondamental du calcul des variations — Le lemme fondamental du calcul des variations est un lemme essentiel au calcul des variations. Sommaire 1 Énoncé 2 Preuve 3 Lemme de du Bois Reymond 4 Applications … Wikipédia en Français
Calcul Des Variations — En analyse fonctionnelle, le calcul des variations (ou calcul variationnel) est un ensemble de méthodes permettant de déterminer les points critiques ou les extrémales de fonctionnelles à l aide de l équation d Euler Lagrange. L application des… … Wikipédia en Français
Calcul des variations — En analyse fonctionnelle, le calcul des variations (ou calcul variationnel) est un ensemble de méthodes permettant de déterminer les points critiques ou les extrémales de fonctionnelles à l aide de l équation d Euler Lagrange. L application des… … Wikipédia en Français
VARIATIONS (CALCUL DES) — L’étude d’une fonction à valeurs réelles comporte en particulier la détermination de ses extrémums. C’est là un des objets du calcul différentiel classique lorsque la source de cette fonction est un espace numérique; c’est l’objet de ce qu’Euler… … Encyclopédie Universelle
Calcul variationnel — Calcul des variations En analyse fonctionnelle, le calcul des variations (ou calcul variationnel) est un ensemble de méthodes permettant de déterminer les points critiques ou les extrémales de fonctionnelles à l aide de l équation d Euler… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Théorème fondamental — En mathématiques, un théorème fondamental est un théorème essentiel à une branche et qui permet d établir de nouveaux théorèmes sans s appuyer sur des axiomes. Plusieurs de ces théorèmes doivent leur nom à la tradition et non à la branche qui l… … Wikipédia en Français
Theoreme fondamental — Théorème fondamental En mathématiques, un théorème fondamental est un théorème essentiel à une branche et qui permet d établir de nouveaux théorèmes sans s appuyer sur des axiomes. Plusieurs de ces théorèmes doivent leur nom à la tradition et non … Wikipédia en Français
Géométrie différentielle des surfaces — En mathématiques, la géométrie différentielle des surfaces est la branche de la géométrie différentielle qui traite des surfaces (les objets géométriques de l espace usuel E3, ou leur généralisation que sont les variétés de dimension 2), munies… … Wikipédia en Français
![h\in C^\infty [a,b]](/pictures/frwiki/102/fee43d4ace98a758497786f58013b0e7.png) avec h(a) = h(b) = 0, alors f(x) est identiquement nulle sur l'intervalle ouvert (a,b).
avec h(a) = h(b) = 0, alors f(x) est identiquement nulle sur l'intervalle ouvert (a,b).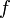 localement intégrable sur un ensemble ouvert U de
localement intégrable sur un ensemble ouvert U de 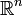 et les fonctions h sont de classe
et les fonctions h sont de classe 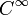 et à support compact dans U (La conclusion est changée par « f est nulle presque partout »).
et à support compact dans U (La conclusion est changée par « f est nulle presque partout »).