Lemme De Zolotarev

Lemme de Zolotarev

En mathématiques, le lemme de Zolotarev est un résultat d'arithmétique modulaire énonce que le symbole de Legendre

$\left(\frac{a}{p}\right)$

pour un entier a modulo un nombre premier p, peut être calculé de la manière suivante:

ε(π_a)

avec ε désignant la signature d'une permutation et π_a la permutation de la classe des résidus mod p qui multiplie chaque élément par a, à condition que p ne divise pas a.

Preuve

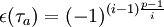Un élément non nul a du corps fini à p éléments agit par multiplication à droite sur le groupe multiplicatif de ce corps. Il est facile de voir que cette action admet (p-1)/i orbites, chacune de taille i, où i est l'ordre de a (c'est-à-dire le plus petit entier tel que $a i = 1$ ). La signature de cette action est alors $\epsilon(\tau_a)=(-1)^{(i-1)\frac{p-1}{i}}$ .

On discute alors suivant la parité de i : si i est pair alors 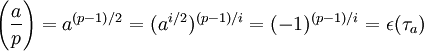$\left (\frac{a}{p}\right)=a^{(p-1)/2}=(a^{i/2})^{(p-1)/i}=(-1)^{(p-1)/i}=\epsilon(\tau_a)$ ; si i est impair alors 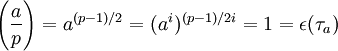$\left (\frac{a}{p}\right)=a^{(p-1)/2}=(a^{i})^{(p-1)/2i}=1=\epsilon(\tau_a)$ . Dans les deux cas, c'est le résultat attendu.

Historique

Ce lemme a été introduit par Egor Ivanovich Zolotarev en 1872 pour une preuve de la Loi de réciprocité quadratique.

Voir aussi : lemme de Gauss.

Référence

E. Zolotarev, Nouvelle démonstration de la loi de réciprocité de Legendre, Nouv. Ann. Math (2), 11 (1872), 354-362

Liens externes

PlanetMath page

Portail des mathématiques

Ce document provient de « Lemme de Zolotarev ».

Catégories : Arithmétique modulaire | Permutation | Lemme de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme De Zolotarev de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Lemme de zolotarev — En mathématiques, le lemme de Zolotarev est un résultat d arithmétique modulaire énonce que le symbole de Legendre pour un entier a modulo un nombre premier p, peut être calculé de la manière suivante: ε(πa) avec ε désignant la signature d une… … Wikipédia en Français
Lemme de Zolotarev — En mathématiques, le lemme de Zolotarev est un résultat d arithmétique modulaire équivalent au lemme de Gauss et introduit par Yegor Ivanovich Zolotarev (en) en 1872 pour redémontrer la loi de réciprocité quadratique. Il énonce que pour tout … Wikipédia en Français
Lemme de Gauss (théorie des nombres) — Pour les articles homonymes, voir Théorème de Gauss. Le lemme de Gauss en théorie des nombres donne une condition pour qu un entier soit un résidu quadratique. Il a été introduit et démontré par Gauss dans ses preuves de la loi de réciprocité… … Wikipédia en Français
Liste des lemmes (mathematiques) — Liste des lemmes (mathématiques) Liste des lemmes mathématiques par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom des lemmes comprend des noms de scientifiques, on se base sur le… … Wikipédia en Français
Liste des lemmes (mathématiques) — Liste des lemmes mathématiques par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom des lemmes comprend des noms de scientifiques, on se base sur le premier nom propre cité. Si le nom … Wikipédia en Français
Liste de lemmes (mathématiques) — Liste de lemmes mathématiques par ordre alphabétique. En mathématiques, un lemme est un énoncé prouvé, mais jugé moins important que ce qu on appelle un théorème, qu il sert généralement à établir au cours d une démonstration. Néanmoins cette… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Loi de réciprocité quadratique — En mathématiques, et plus précisément en théorie algébrique des nombres, la loi de réciprocité quadratique, conjecturée par Euler et Legendre et correctement démontrée pour la première fois par Gauss, établit un lien entre la résolubilité de deux … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Lemme De Zolotarev