- Jauge de déformation
-
Le but des extensomètres à fils résistants ou jauges de déformation (strain gauge) est de traduire la déformation d'une pièce en variation de résistance électrique (plus les extensomètres s'étirent, plus leurs résistances augmentent). Elles consistent en des spires rapprochées et sont généralement fabriquées à partir d'une mince feuille métallique (quelques µm d'épaisseur) et d'un isolant électrique, que l'on traite comme un circuit imprimé (par lithographie ou par attaque à l'acide).
Sommaire
Présentation de la relation contrainte-déformation
Une contrainte est l'état de pression dans lequel se trouve un matériau lorsqu'on lui applique une ou plusieurs forces. Il s'agit d'une réaction distribuée de la matière, les atomes se réorganisent pour compenser les forces extérieures.
Une contrainte est une force divisée par une surface, elle est donc homogène à une pression et exprimée en pascals.
On peut distinguer différents types de déformations :
- la déformation élastique, qui est réversible
- la déformation plastique, qui ne l'est pas
- Le fluage qui est une déformation irréversible qui augmente avec le temps sous l'effet d'une contrainte constante. La vitesse de fluage augmente généralement lorsque la température du matériau augmente.
Déformation élastique
L'exemple le plus parlant d'une déformation élastique est le cas du ressort.
La déformation élastique est une déformation réversible : le milieu retourne à son état initial lorsque l'on supprime les sollicitations.
L'élasticité linéaire concerne les petites déformations proportionnelles à la sollicitation. Dans cette gamme, l'allongement est proportionnel à la force dans le cas d'un étirement, et l'angle est proportionnel au couple dans le cas d'une torsion.
Aux plus grandes déformations, l'élasticité devient non linéaire pour certains matériaux (déformation plastique). Pour d'autres, la fracture ou le fluage interviennent. La déformation élastique intervient pour les faibles sollicitations. Si l'on augmente les sollicitations, on change le mode de déformation :
- Rupture (endommagement) pour les matériaux dits « fragiles »
- Déformation plastique (irréversible et non linéaire) puis rupture pour les matériaux dits « ductiles » ;
- Éventuellement fluage pour les matériaux ductiles si la vitesse de déformation est lente et/ou la température élevée.
Déformation plastique
La déformation plastique est la déformation irréversible d'une pièce ; elle se produit par un réarrangement de la position des atomes.
Lorsque que l'on sollicite une pièce ou un objet (on le tire, on le comprime, on le tord...), celui-ci commence par se déformer de manière réversible (déformation élastique), c'est-à-dire que ses dimensions changent, mais il reprend sa forme initiale lorsque la sollicitation s'arrête. Ensuite, si les sollicitations continuent on dépasse la déformation élastique pour entrer dans la déformation plastique. Certains matériaux, dits « fragiles », cassent dans ce mode de déformation si la sollicitation est trop forte.
Pour les matériaux dits « ductiles », lorsque l'on augmente la sollicitation, on déforme de manière définitive la pièce : lorsque l'on arrête la sollicitation, la pièce reste déformée. Ceci se produit par un glissement des plans atomiques les uns sur les autres, à la manière des cartes à jouer d'un paquet. Ce glissement de plans atomiques se fait grâce au déplacement de défauts linéaires localisés appelés « dislocations ».
Lorsqu'une pièce est entrée dans la zone de déformation plastique et que l'on supprime la sollicitation, sa déformation (finale) diminue toutefois par rapport à la forme sous charge, car la déformation correspondant à la zone élastique disparait (seule la déformation plastique a un effet permanent sur la pièce). Une petite expérience à faire pour visualiser ce phénomène : essayez de plier (et non uniquement cintrer) une tôle métallique : bloquez un côté de la tôle et essayez de la plier jusqu'à un repère choisi. Pour que la plaque, une fois relâchée, soit alignée avec ce repère, il faut appliquer une sollicitation qui déplace la tôle au delà du repère. Lorsque l'on relâche la tôle, celle-ci 'recule' alors jusqu'au repère. Une fois pliée, on peut d'ailleurs de nouveau déformer légèrement cette tôle (en restant dans la 'zone élastique') et elle reviendra en face du repère. La zone élastique existe donc toujours.
Fluage
On appelle fluage d'un matériau le phénomène de déformation irréversible qui augmente avec le temps sous l'effet d'une contrainte constante.
La vitesse de fluage augmente généralement lorsque la température du matériau augmente.
La déformation par fluage peut se modéliser comme un frottement fluide, du type amortisseur de suspension de voiture. De la même manière que pour la déformation plastique, le fluage est toujours associé à la déformation élastique. On peut voir le fluage comme un « retard à la déformation » : si l'on impose une déformation, on a d'abord une réponse élastique, puis, pour une vitesse de déformation maintenue constante, la force nécessaire à la déformation diminue.
Exemple pratique de liquide de ce type : un pot de miel sortant du réfrigérateur ! On aura du mal à enfoncer une lame de couteau d'un coup jusqu'à la garde dans le miel « refroidi », mais si l'on appuie de manière constante sur le couteau, la vitesse de descente augmentera, malgré une force d'appui constante. De même, si la température du miel augmente, l'effort nécessaire pour enfoncer le couteau diminuera avec l'augmentation de température.
La mesure
Piézorésistance
La piézorésistance est le changement de conductibilité d'un matériau dû à une contrainte mécanique. Elle a été mise en évidence pour la première fois par Lord Kelvin en 1856.
La piézorésistance dans les semi-conducteurs a été découverte sur un cristal de silicium en 1954.
Explication
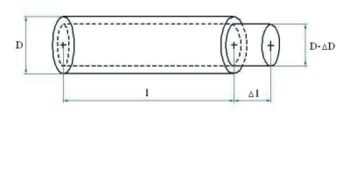
La résistance électrique d'une jauge cylindrique est donnée par :
avec :
- ρ, résistivité du conducteur
- l sa longueur
- A l'aire de sa section
- D, le diamètre de la section.
Donc après déformation de la jauge, on obtient :
On peut alors exprimer la variation relative de la résistance par :
Avec k, la sensibilité d'un appareil piézorésistant, dépend principalement du constituant de la jauge et
 et R représente respectivement la variation relative de longueur et la résistance.
et R représente respectivement la variation relative de longueur et la résistance.Piézorésistance des métaux
La piézorésistance d'un capteur métallique est due au changement de géométrie dû à la contrainte mécanique. Ce facteur géométrique du capteur se représente par la variable k :
où
 représente le coefficient de Poisson du matériau.
représente le coefficient de Poisson du matériau.
Même si les variations sont relativement faibles, elles permettent d'utiliser ces capteurs (jauge de contrainte) sur une large gamme d'utilisation.
Piézorésistance dans les semi-conducteurs
La variable k d'un semi-conducteur peut-être cent fois supérieure à celle des métaux. Les semi-conducteurs généralement utilisés sont le germanium et le silicium (amorphe ou cristallisé).
Une contrainte appliquée sur du silicium va modifier sa conductibilité pour deux raisons : sa variation géométrique mais aussi sur la conductibilité intrinsèque du matériau. Il en résulte une amplitude bien plus importante que pour des capteurs métalliques.
Piézorésistance des capteurs en silicium
La piézorésistance des semi-conducteurs a été utilisée avec un grand nombre de matériaux (germanium, silicium polycristalin ou amorphe…). Le silicium étant aujourd'hui largement utilisé dans les circuits intégrés, l'utilisation des capteurs à base de silicium est largement répandue et permet une bonne intégration des jauges de contraintes avec les circuits bipolaires ou CMOS.
Cela a permis une grande gamme d'utilisation de la piézorésistance. Beaucoup d'appareils commerciaux comme les capteurs d'accélération utilisent des capteurs en silicium.
Piézorésistance ou piézorésistor
Les piézorésistances ou piézorésistors sont des résistances variables faites à partir d'un matériau piézorésistant et sont utilisées pour les jauges de contraintes, couplées avec un pont de Wheatstone.
Application à la mesure
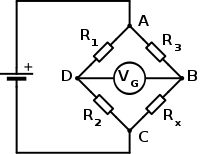
La mesure ne peut s'effectuer directement car les variations de conductibilité de la jauge sont trop faibles pour être mesurées directement avec un ohmmètre. Il est nécessaire de faire un montage en pont de Wheatstone (voir figure à droite).
Soit un circuit constitué de quatre résistances R1,R2,R3,R4 montées en pont. On alimente par une source électromotrice Ve suivant la diagonale AC. À l'équilibre la tension Vs est nulle mais la variation d'une quelconque des résistance fait apparaître une tension Vs entre B et D.
Pour de très faibles variations (de l'ordre du microohms pour les jauges de contraintes), la sortie Vs est proportionnelle aux variations relatives ΔR / R de chacune des résistances. En négligeant les termes d'ordres supérieurs, elle vaut :

Dans la pratique, ces résistances sont souvent d'autres jauges (une, deux ou quatre).
L'alternance des signe + et - caractérise la propriété fondamentale des ponts : deux résistances adjacentes agissent en sens opposé et deux résistances opposées agissent dans le même sens. On peut donc réduire les variations parasites (comme la température) et avoir une meilleure précision.
Un capteur à quatre jauges permet d'avoir encore une meilleure précision qu'un capteur à une jauge. Dans la pratique, le nombre de jauges est souvent dicté par la géométrie de la pièce.
On distingue trois montages différents selon le nombre de jauges mis en place.
Montage
Montage en Quart de pont
Dans le montage en quart de pont, on ne dispose que d'une jauge et trois résistances viennent en complément avec l'électronique associée. Ce montage est le plus simple et le moins cher mais présente de nombreux inconvénients :
- La jauge étant éloignée des autres résistances, il faut prendre en compte la résistance induite par la longueur de câble.
- La tension alimentant la jauge diminue de la somme des variations de tension rencontrées sur les câbles de liaison. À l’entrée de la jauge, elle est largement inférieure à celle qui sort de l’amplificateur. La sensibilité du capteur (qui varie proportionnellement à la tension d’alimentation) s’en trouve alors amoindrie…
- La résistance du câblage ajoute également une atténuation du signal et donc une perte d'information. Par exemple, un câble de 100 m conduit à une variation de 10 %.
Des corrections sont indispensable à ce type de montage tel que l'étalonnage "shunt" du système de mesures.
Montage en demi-pont
Le montage demi-pont est couramment utilisé lorsque l'on souhaite faire des corrections en température sur matériaux à mesurer. Il est aussi utilisé pour supprimer la composante de traction (ou compression) lors de mesures de flexion.
Montage en pont complet
Soit le fil spiralé de longueur L, de diamètre d et de section S. Sa résistance est R=ro
Donc les variations relatives de la résistance s'écrivent :Constituant de la jauge
Selon son utilisation (environnement, précision...), différents matériaux peuvent être utilisés.
Le corps d'épreuve
Le corps d'épreuve est la partie qui subira les déformations. Il est donc préférable d'utiliser un matériau facilement déformable afin d'obtenir un signal de forte amplitude. Il faut également éviter de sortir de la gamme de déformation élastique de celui-ci pour éviter tout risque de déformation permanente.
Certain aciers alliés (E4340 par exemple) donnent une bonne précision et une excellente résistance à la fatigue mais doivent être protégés de la corrosion alors qu'un acier inoxydable n'a pas ce problème mais est moins homogène et donc moins précis. Il est également possible d'utiliser des capteurs en aluminium pour des capteurs de faibles capacités.
Le support
Le support fait le lien entre le corps d'épreuve et la pièce déformée. Il doit donc répondre à des caractéristiques bien spécifiques : déformation facile, bonne aptitude au collage et un coefficient de variation relativement faible. On peut ici utiliser des résines époxydes ou des polyimides.
La colle
Elle réalise la liaison entre le support de la jauge et le corps d'épreuve. Elle a également le rôle d'isolant. La colle est choisie en fonction du support.
La jauge
Le matériau composant les jauges doit avoir une bonne résistance à la fatigue une aptitude au soudage et une bonne tenue en température. On utilise les matériaux suivants :
- Constantan (alliage 55% Cu, 45% Ni), couramment utilisé. Il supporte des températures de 200 °C.
- Karma (alliage 74 Ni, 20 Cr, 3% Cu, 3% Fe), meilleure sensibilité et peut être utilisé jusqu'à 350 °C.
- Platine – Tungstène (92% Pt, 8% W), plus cher mais présente une meilleure résistance à la fatigue. Il reste donc pour des utilisations spécifiques.
- Semi-conducteurs (Silicium). Ils ont une sensibilité bien meilleure (50 à 100 fois plus) mais ont une moins bonne linéarité et sont plus sensibles aux variations de température.
Effets parasites
Température
D'une part, la dilatation différentielle entre jauge et support, d'autre part, les effets thermoélectriques liés à un écart de température entre deux points de raccordement (on peut éliminer ce problème en alimentant les jauges en alternatif).
Pour minimiser l'influence de la température, on peut utiliser une configuration en double pont. Une jauge active, soumise à la déformation et aux variations de température, et une jauge passive soumise uniquement aux variations de température.
En pratique, pour corriger les dérives de pente (sensibilité) en température, on place dans les deux branches d'alimentation une résistance en Nickel pur. Ces résistances vont modifier la tension d'alimentation aux bornes du pont de manière à compenser la dérive thermique.
La dérive du signal à vide est un autre phénomène lié à la température (sans contrainte mécanique sur le corps d'épreuve). Cette dérive est aléatoire et est intrinsèque au pont de jauges. La correction se fait sur une branche du pont (dépendant du sens de la dérive) par l'ajout d'un bobinage de cuivre (lui-même va occasionner une dérive contraire à celle des jauges).
Hystérésis
Un capteur présente un phénomène d’hystérésis si l’information qu’il délivre est différente suivant que les mesures sont effectuées sous charge croissante ou décroissante. Cette source d’erreur est donc particulièrement gênante dans le cas de cycles de mesures avec montée et descente en charge répétées, ou en fonctionnement dynamique. L’hystérésis peut être positive ou négative. Contrairement à l’écart de linéarité, il n’est pas aussi simple de la compenser avec l’électronique de mesure. Il s’agit en effet d’une caractéristique liée aux matériaux constituant le corps d’épreuve et à la liaison corps d’épreuve-détecteur. Les aciers inoxydables, par exemple, présentent une hystérésis positive importante et des traitements thermiques sont nécessaires afin de limiter ce phénomène. On peut aussi contrôler la dureté des feuilles de constantan.
Erreur de linéarité
Un capteur présente une erreur de linéarité lorsque la courbe force-signal capteur n'est pas une droite parfaite. L'erreur de linéarité d'un capteur de force dépend du design du capteur (par exemple, lorsque la force croît, la répartition des forces varie ce qui influence la linéarité), mais aussi du choix des jauges. L'erreur de linéarité est toujours à minimiser. En production de série, le capteur est calibré en passant par deux points : le zéro et la force nominale. En minimisant l'erreur de linéarité, cette calibration suffit. Si l'erreur de linéarité est importante, il est nécessaire de passer par plusieurs points intermédiaires d'étalonnages.
Fonctionnement des capteurs de force à jauges de contrainte
Un capteur de force est constitué de jauges de contrainte de déformation identique. Le principe étant de traduire en variation de résistance électrique la déformation du corps d’épreuve sur lequel elles sont collées.
Principe de fonctionnement des jauges de contraintes
Le fonctionnement des capteurs à jauges de contraintes est fondé sur la variation de résistance électrique de la jauge proportionnellement à sa déformation. C’est le coefficient ou facteur de jauge k qui traduit cette proportionnalité, suivant la relation :
Delta(R) / R = kDelta(L) / L k est une constante qui dépend des matériaux considérés et de la température. Elle caractérise la sensibilité de la jauge.
Le corps d’épreuve du capteur de force
Il existe différentes formes de capteurs à jauges : Les capteurs de force en « S » pour des mesure en traction / compression. Les capteurs de force « pancake » pour des mesures en traction / compression. Les pesons de compression standard ou miniature. Les capteurs à moment contant ou à cisaillement utilisés pour des applications de pesage…
Les matériaux utilisés
Les aciers alliés. Les aciers inoxydables utilisé en milieu corrosif. Les alliages d’aluminium. En fonction du choix du matériau et de la forme du capteur, la déformation mesurée sera importante et l’amplitude du signal de sortie élevé.
Les effets parasites
Les variations de température. Les variations de température entraînent deux conséquences majeures: la dilatation des matériaux et une variation de résistances des jauges.
Dérive thermique du zéro
En l’absence de contrainte, la résistance augmente avec la température. Le signal même très proche de zéro, n’est pas nul. Cette dérive est aléatoire et est intrinsèque au pont de jauges.
Effet thermique sur la sensibilité
L’élasticité du corps d’épreuve ainsi que le coefficient de jauge (k) dépendent de la température. Cela implique une variation de la sensibilité.
Le fluage
Il s’agit de la déformation du corps d’épreuve soumis à une force constante avec le temps.
L’hystérésis
Un capteur de force présente un phénomène d’hystérésis si l’information qu’il délivre est différente suivant que les mesures sont effectuées en traction ou en compression.
L’écart de linéarité
L’information délivrée en sortie n’est pas toujours proportionnelle à la valeur d’entrée. Un capteur présente une erreur de linéarité lorsque la courbe force / signal du capteur n'est pas une droite parfaite.
Voir aussi
- Portail de la physique
- Portail de l’électricité et de l’électronique
- Portail des micro et nanotechnologies
Wikimedia Foundation. 2010.