- Inégalité de Poincaré-Wirtinger
-
Inégalité de Poincaré
En mathématiques, l'Inégalité de Poincaré (du nom du mathématicien français Henri Poincaré) est un résultat de la Théorie des espaces de Sobolev.
Cette inégalité permet de borner une fonction à partir d'une estimation sur ses dérivées et de la géométrie de son domaine de définition. Ces estimations sont d'une grande importance pour la méthode moderne directe du calcul des variations. Un résultat voisin est l' inégalité de Friedrichs.
Sommaire
L'inégalité de Poincaré classique
Soit p, tel que 1 ≤ p < ∞ et Ω un ouvert de largeur finie (borné dans une direction). Alors il existe une constante C, dépendant uniquement de Ω et p , telle que, pour toute fonction u de l'espace de Sobolev W01,p(Ω),
L'inégalité de Poincaré-Wirtinger
Soit p, tel que 1 ≤ p ≤ ∞ et Ω un ouvert borné de l'espace euclidien de dimension n Rn possédant une frontière Lipschitzienne (par conséquent Ω est un domaine Lipschitzien borné ouvert). Alors il existe une constante C, dépendant uniquement de Ω et p, telle que, pour toute fonction u de l'espace de Sobolev W1,p(Ω),
où
est la valeur moyenne de u sur Ω, et |Ω| représente la mesure de Lebesgue du domaine Ω.
L'inégalité de Wirtinger
Généralisations
L'inégalité de Poincaré peut se généraliser à d'autres espaces de Sobolev. Par exemple, l'inégalité de Poincaré suivante (extraite de Garroni & Müller (2005)) est associée à l'espace de Sobolev H1/2(T2), c.à.d l'espace des fonctions u de l' espace L2 du tore unitaire T2 avec comme transformée de Fourier la fonction û satisfaisant
il existe alors une constante C telle que, quel que soit u ∈ H1/2(T2) avec u uniformément nul sur un ensemble ouvert E ⊆ T2,
où cap(E × {0}) représente la capacité harmonique de E × {0} lorsque considéré comme sous-ensemble de R3.
Constante de Poincaré
La constante optimale C dans l'inégalité de Poincaré est parfois appelée Constante de Poincaré du domaine Ω. En général, déterminer la constante de Poincaré est une tâche très difficile qui dépend de la valeur de p et de la géométrie du domaine Ω. Certains cas particuliers peuvent cependant être résolus. Par exemple, si Ω est un domaine Lipschitzien borné, convexe de diamètre d, alors la constante de Poincaré vaut d/2 pour p = 1, d/π pour p = 2; (Acosta and Durán 2004). En dimension un, c'est l'Inégalité de Wirtinger appliquée aux fonctions.
Cependant il est possible de déterminer concrètement la constante C pour certains cas particuliers. Par exemple, pour p = 2, il est bien connu que sur le domaine du triangle isocèle rectangle unitaire, C = 1/π( < d/π où
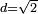 ). (cf., par exemple,« Kikuchi & Liu 2007 ».)
). (cf., par exemple,« Kikuchi & Liu 2007 ».)Notes et références
- (ang) Acosta, Gabriel, Durán, Ricardo G., « An optimal Poincaré inequality in L1 for convex domains », dans Proc. Amer. Math. Soc., vol. 132, no 1, p. 195–202 (electronic) [lien DOI]
- (ang) Evans, Lawrence C., « Partial differential equations », dans American Mathematical Society, vol. 132, no 1 (ISBN ISBN 0-8218-0772-2)
- (ang) Garroni, Adriana, Müller, Stefan, « Γ-limit of a phase-field model of dislocations », dans SIAM J. Math. Anal., vol. 36, 2005, p. 1943–1964 (electronic) [lien DOI]
- (ang) Fumio, Kikuchi, Xuefeng, Liu, « Estimation of interpolation error constants for the P0 and P1 triangular finite elements », dans Comput. Methods. Appl. Mech. Engrg., vol. 196, 2007, p. 3750–3758 (ISSN 0045-7825) [lien DOI]
- Portail des mathématiques
Catégories : Inégalité | Espace de Sobolev
Wikimedia Foundation. 2010.

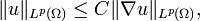
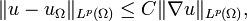
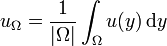
![[ u ]_{H^{1/2} (\mathbf{T}^{2})}^{2} = \sum_{k \in \mathbf{Z}^{2}} | k | \big| \hat{u} (k) \big|^{2} < + \infty:](/pictures/frwiki/52/4bf5bd79e3ea78e00d33bfa1255c536f.png)
![\int_{\mathbf{T}^{2}} | u(x) |^{2} \, \mathrm{d} x \leq C \left( 1 + \frac1{\mathrm{cap} (E \times \{ 0 \})} \right) [ u ]_{H^{1/2} (\mathbf{T}^{2})}^{2},](/pictures/frwiki/53/5fcdf26b722555d66002d13744debfca.png)