Intensité spécifique

Intensité spécifique
Page d'aide sur l'homonymie Pour les articles homonymes, voir Intensité.
Définition de l'intensité spécifique

En astronomie, l'intensité spécifique est une grandeur physique qui décrit le rayonnement électromagnétique qui traverse une région donnée.

Cette quantité dépend du point et de l'instant considéré, mais aussi de la fréquence du rayonnement et de la direction dans laquelle il se propage. L'intensité spécifique joue un rôle central dans l'étude de tous les processus faisant intervenir la propagation de la lumière quand celle-ci interagit avec le milieu dans lequel elle se trouve. Le transfert radiatif (ou transfert de rayonnement) est la discipline qui étudie l'évolution de l'intensité spécifique et des quantités associées.

Sommaire

Formule

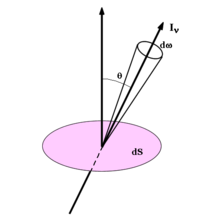
L'intensité spécifique, traditionnellement notée Iν, désigne l'amplitude de la grandeur qui intervient dans la détermination de la quantité d'énergie dE sous forme de photons, dont la fréquence est égale à ν à dν près, et qui traverse une petite surface dA pendant l'intervalle de temps dt dans une direction centrée sur un angle solide dω.

Si l'on considère des échelles de temps et de distances telles que la répartition du rayonnement ne change pas, alors l'énergie dE considéré est proportionnelle à la durée dt considérée, ainsi qu'à la surface dA et l'intervalle dν et l'angle solide dω. L'on peut ainsi noter sans perte de généralité

{\rm d} E = I_\nu \cos \theta \; {\rm d} A \; {\rm d}t \; {\rm d}\omega \; {\rm d}\nu,

où θ représente l'angle entre la normale à la surface dA considérée et la direction de l'angle solide dω. La présence du facteur cos θ est motivée par le fait que la portion de rayonnement qui traverse effectivement la surface considérée est déterminée par la projection de cette surface perpendiculairement à la direction du rayonnement, projection qui vaut dA cos θ. Avec cette définition, Iν ne dépend de l'orientation de la surface que par le facteur cos θ. En particulier, un rayonnement isotrope se caractérise par un Iν constant.

L'unité du système international de l'intensité spécifique est le watt par mètre carré par hertz et par stéradian. L'usage en astrophysique étant plutôt d'utilisé le système CGS, l'intensité spécifique est souvent exprimée en erg par seconde, par centimètre carré par hertz et par stéradian. L'intensité spécifique dépend du point x et de la direction n de propagation du rayonnement considérés, ainsi que du temps t et de la fréquence ν. On omet cependant d'écrire ces dépendance, et on ne note, sauf cas particulier que la dépendance en fréquence (Iν plutôt que I(x, t, ν, n)).

Exemple

Un corps noir est le nom donné à un objet qui se trouve être en équilibre thermique avec le rayonnement dans lequel il baigne. Dans ce cas, on peut montrer que l'intensité spécifique suit une loi qui ne dépend que d'un seul paramètre, la température (plus précisément la température thermodynamique) T. L'intensité spécifique d'un corps noir est traditionnellement notée Bν plutôt que le traditionnel Iν, et elle est déterminée par la formule dite loi de Planck, du nom du physicien allemand Max Planck :

B_\nu(T) = \frac{2 h \nu^3}{c^2} \frac{1}{{\rm e}^{\frac{h \nu}{k_{\rm B} T}} - 1},

où h désigne la constante de Planck, c la vitesse de la lumière, kB la constante de Boltzmann.

Autre écriture

Sans perte de généralité, on peut exprimer l'intensité spécifique par unité de longueur d'onde plutôt que par unité de fréquence. On définit dans ce que la quantité notée Iλ par la relation

Iλ | dλ | = Iν | dν | ,

en utilisant la relation ordinaire entre longueur d'onde λ et fréquence ν, soit

\lambda = \frac{c}{\nu},

ce qui donne

{\rm d}\lambda = - \frac{c}{\lambda^2} {\rm d} \nu,

et au final

I_\lambda = \frac{c}{\lambda^2} I_\nu.

Ainsi, pour un corps noir, on a

B_\lambda (T) = \frac{2 h c^2}{\lambda^5} \frac{1}{{\rm e}^{\frac{h c}{\lambda k_{\rm B} T}} - 1}.

Utilisation

À partir de l'intensité spécifique, on peut définir l'intensité totale en intégrant sur l'ensemble des fréquences. On peut aussi déterminer une quantité directement observable, la densité de flux (souvent improprement appelée « flux » en intégrant sur les directions possibles (c'est-à-dire sur l'angle solide dω). La densité d'énergie du rayonnement se déduit également à partir de l'intensité spécifique.

Voir aussi

Référence


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Intensité spécifique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • intensité spécifique — savitasis stipris statusas T sritis fizika atitikmenys: angl. specific strength vok. spezifische Intensität, f rus. удельная интенсивность, f pranc. intensité spécifique, f …   Fizikos terminų žodynas

  • Intensite — Intensité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Intensité — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Intensité », sur le Wiktionnaire (dictionnaire universel) Le terme d intensité désigne en général l… …   Wikipédia en Français

  • Intense — Intensité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Température effective — Transfert de rayonnement Le transfert de rayonnement est le domaine de la physique décrivant l interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d analyser la propagation de la lumière à travers un… …   Wikipédia en Français

  • Transfert de rayonnement — Le transfert de rayonnement est le domaine de la physique décrivant l interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d analyser la propagation de la lumière à travers un milieu gazeux et joue de… …   Wikipédia en Français

  • Transfert du rayonnement — Transfert de rayonnement Le transfert de rayonnement est le domaine de la physique décrivant l interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d analyser la propagation de la lumière à travers un… …   Wikipédia en Français

  • Transfert radiatif — Transfert de rayonnement Le transfert de rayonnement est le domaine de la physique décrivant l interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d analyser la propagation de la lumière à travers un… …   Wikipédia en Français

  • Densite de flux — Densité de flux En astrophysique, on appelle densité de flux la mesure du flux d énergie sous forme de rayonnement électromagnétique par unité de fréquence passant à travers une surface donnée. Le terme ambigu de « densité » se réfère… …   Wikipédia en Français

  • Densité De Flux — En astrophysique, on appelle densité de flux la mesure du flux d énergie sous forme de rayonnement électromagnétique par unité de fréquence passant à travers une surface donnée. Le terme ambigu de « densité » se réfère au fait que l on… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”