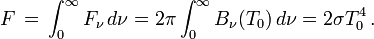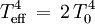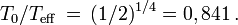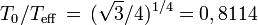- Température effective
-
Transfert de rayonnement
Le transfert de rayonnement est le domaine de la physique décrivant l'interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d'analyser la propagation de la lumière à travers un milieu gazeux et joue de ce fait un rôle fondamental dans les diagnostics effectués en astrophysique à partir des spectres stellaires.
Sommaire
Problématique
Dans de nombreuses circonstances il est nécessaire de déterminer les propriétés intrinsèques d'un objet à partir du rayonnement observé. C'est le cas en astrophysique puisque les objets célestes sont bien trop lointains pour offrir la possibilité d'aller mesurer leurs propriétés physiques in situ. De ce fait il est nécessaire de modéliser :
- l'émission de rayonnement en tout point de l'objet en fonction des propriétés locales comme par exemple la température et la densité,
- la manière dont le rayonnement est transmis par la matière située entre le point d'émission et l'observateur terrestre.
Cette étude constitue le transfert du rayonnement.
Comme exemple simple d'action de la matière sur la lumière, le soleil est de couleur rouge au coucher et au lever non pas parce qu'il change intrinsèquement de couleur mais parce que traversant une couche plus importante d'air diffusant préférentiellement le bleu et le violet[1] ses rayons lumineux laissent au contraire passer plus facilement l'orange et le rouge.
De façon plus générale la lumière des astres est reçue sous forme de spectres donnant la répartition de la lumière en fonction de la longueur d'onde. Le transfert de rayonnement a pour objet de calculer le spectre théorique émis par un modèle numérique d'étoile en fonction de ses caractéristiques physiques, comme sa température, sa taille, sa masse, etc. En sens inverse, c'est en comparant les spectres observés aux spectres théoriques que l'on pourra déterminer les propriétés physiques d'une étoile. Comme en astrophysique toute l'information est contenue dans les spectres la justesse du diagnostic physique dépend de façon cruciale de la qualité de la théorie du transfert utilisée.
Généralités
Le rayonnement en un point du milieu peut
- subir une absorption, contribuant à chauffer le gaz ;
- subir une diffusion, susceptible de changer sa direction et sa fréquence ;
- être émis par les particules du gaz.
Le rayonnement subit ainsi une variation quantitative et qualitative au cours de sa propagation, ce qui se traduit par une équation différentielle contenant des dérivées par rapport aux variables de position et de temps : l'équation de transfert du rayonnement.
Le rayonnement dépend de
- trois variables de position,
- deux variables de direction,
- une variable de temps,
- une variable de longueur d'onde,
soit sept variables au total. Cette multiplicité de paramètres rend difficile la résolution générale du transfert du rayonnement tant d'un point de vue théorique que numérique. De plus, le rayonnement a une influence sur la matière traversée (chauffage, donc modification de la structure) qui influe rétroactivement sur le rayonnement (émission). Il s'ensuit que le problème est non linéaire et doit être résolu de manière itérative dans la plupart des cas.
Dans un grand nombre de situations l'échelle de temps radiative est très courte par rapport à l'échelle de temps thermique, de sorte que l'on peut supposer le transfert de rayonnement comme quasi-statique, éliminant ainsi la variable temporelle. Cette condition est parfois réalisée dans des expériences sur Terre mais pas toujours en astrophysique où les diverses échelles de temps et de distance peuvent devenir considérables. Cependant, par souci de simplicité, c'est surtout dans le cadre de cette hypothèse statique, à vérifier dans chaque circonstance particulière, que se fera le reste de cette présentation. Dans d'autres cas, le nombre de variables de position peut être réduit à deux ou à une seule si la géométrie du système s'y prête. Enfin, si l'on utilise parfois des valeurs bolométriques pour le rayonnement afin d'éliminer la variable de longueur d'onde, cette approximation peut s'avérer difficile à justifier lorsqu'il s'agit de construire un spectre en longueur d'onde. Toutefois l'approximation du cas gris mentionnée ci-dessous, qui consiste à ignorer la variation des propriétés d'absorption du milieu avec la longueur d'onde, permet d'obtenir des résultats intéressants.
Ajoutons enfin que la présentation faite ici ignore la polarisation de la lumière, un phénomène qui compliquerait encore les choses mais dont l'importance est pourtant grande en astrophysique car son analyse permet de faire des diagnostics sur la structure et la force du champ magnétique.
Intensité de rayonnement
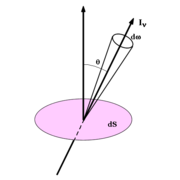
En astrophysique on caractérise le rayonnement par son intensité Iν (ou intensité spécifique) définie de la façon suivante. En un point donné de l'espace on considère un rayonnement contenu dans un angle solide dω, dans un intervalle de fréquence de ν à ν + dν et traversant une aire élémentaire dσ perpendiculaire à sa direction de propagation. Pour abréger la rédaction par la suite nous appellerons « photons (ou rayonnement) de classe A » les photons que nous venons de définir ainsi (c'est-à-dire traversant une surface dσ pendant le temps dt et contenus dans l'angle solide dω et dans l'intervalle de fréquence dν). La quantité d'énergie dEν des photons de classe A est proportionnelle à dσ dν dω dt, ce que l'on peut écrire :
La quantité Iν ainsi introduite est l'intensité du rayonnement : c'est donc l'énergie par unité d'aire, par unité de temps, par unité de fréquence, par unité d'angle solide, traversant une surface perpendiculaire au faisceau de rayonnement. La quantité (Iν dν) s'exprime en erg⋅s-1⋅cm-2⋅sr-1 dans le système CGS (utilisé de coutume en astrophysique), ou en W⋅m-2⋅sr-1 dans le système SI.
Attention : si on se réfère à la longueur d'onde et non pas à la fréquence, la quantité I λ n'est pas égale à I ν et n'a pas les mêmes dimensions physiques. On a en fait
et, puisque ν = c / λ,
Il résulte de ces formules que I ν se mesure en erg⋅s-1⋅cm-2⋅sr-1·Hz-1. L'unité courante en astrophysique pour I λ est le erg⋅s-1⋅cm-2⋅sr-1·Å-1 car on a l'habitude de mesurer les longueurs d'onde (du visible) en angström.
Si maintenant la surface traversée est donnée et que l'angle θ que fait la direction du rayonnement avec la normale à cette surface varie (voir la figure), la surface de l'aire perpendiculaire au rayonnement est égale à dS cosθ de sorte que la formule donnant l'énergie du rayonnement de classe A devient
Comme indiqué plus haut l'intensité du rayonnement est fonction du point considéré, de la direction, de la fréquence et éventuellement du temps. Autrement dit en réalité, de façon générale,
D'un point de vue microscopique on peut caractériser le rayonnement par la densité de photons Ψ ν. En tenant compte du fait que les photons de classe A possèdent l'énergie h ν et sont contenus dans un cylindre de longueur c dt, on peut réécrire l'énergie de ces photons sous la forme :
On en déduit la densité de photons
Dans une description cinétique du gaz de photons, adaptée à une analyse dans le cadre de l'espace-temps de la relativité générale, on fait plutôt intervenir la densité de photons f par unité de volume dans l'espace des phases (appelée encore fonction de distribution des photons). Comme le moment cinétique d'un photon de fréquence ν se propageant dans la direction
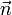 est
estl'élément de volume dans l'espace des phases est
On peut donc écrire le nombre de photons par unité de volume dans l'intervalle dν et dans l'angle solide dω sous la forme
On en déduit que la fonction de distribution des photons s'exprime en fonction des autres grandeurs comme :
La conservation du nombre de photons le long du trajet de la lumière implique donc que la quantité
est un invariant relativiste.
Si le rayonnement est celui d'un corps noir, l'intensité lumineuse suit la loi de Planck et on a
et
On comprend sur cette expression comment s'interprète le rayonnement cosmologique diffus à 3 K. Ce rayonnement est constitué des photons qui ont été émis il y a quelque 14 milliards d'années, environ 300 000 ans après le Big Bang, sous la forme d'un corps noir de 4 500 kelvins, température égale à celle de la matière à cette époque. Depuis les photons ont évolué librement, chacun selon sa propre ligne d'univers, en conservant une répartition de Planck mais avec une diminution constante de la température inversement proportionnelle à la taille croissante de notre Univers. Pour des photons donnés, l'expression de f montre que le nombre de ces photons est conservé, et que si leur fréquence ν diminue au cours du temps, ce qui est le cas, la température T diminue aussi dans les mêmes proportions de telle sorte que le rapport hν/kT reste constant. L'Univers est environ 1 500 fois plus grand qu'à l'époque de l'émission du rayonnement de sorte que sa température est 4500/1500 = 3 (les nombres donnés sont approximatifs mais d'un ordre de grandeur parfaitement correct). Corrélativement la fréquence des photons a été divisée par 1 500 et la longueur d'onde multipliée par 1 500.
Moments de l'intensité
L'intensité caractérise l'énergie traversant une surface dans une direction. L'intégration de cette intensité sur les angles avec pondération par une certaine puissance du cosinus μ de la direction angulaire conduit à la définition de grandeurs physiques importantes et significatives.
L’intensité moyenne est la moyenne de l'intensité sur tout l'angle solide et s'exprime donc sous la forme
Si le rayonnement est isotrope (I ne dépend pas de l'angle, ce qui peut être valable dans des couches profondes de l'étoile), on a évidemment
Le flux à travers une surface est le moment d'ordre 1 de l'intensité, c'est-à-dire la quantité
Physiquement, H représente le flux d'énergie traversant une surface donnée perpendiculaire à un rayon issu du centre de l'étoile. En effet, si on considère cette surface élémentaire dS, la quantité d'énergie du faisceau le traversant dans la direction θ sera proportionnelle à cosθ selon la formule définissant l'intensité. Le flux est donc
Comme le cosinus change de signe lorsque l'angle θ varie entre 0 et π, on voit que le flux est en réalité, physiquement parlant, la différence entre deux quantités : le flux d'énergie correspondant aux rayons lumineux dirigés vers l'extérieur de l'étoile et le flux des rayons dirigés vers l'intérieur de l'étoile. Autrement dit (on suppose d'ordinaire que l'intensité ne dépend pas de l'azimut φ)
Il est d'usage en astrophysique de poser
Avec cette notation l'intensité moyenne devient
et le flux,
ou encore
avec
en distinguant entre un faisceau sortant I+ et un faisceau entrant I -.
Si on se place à la surface d'une étoile et si on suppose que l'intensité émergente ne dépend pas de la direction du faisceau (ce qui est d'ailleurs faux en général) et qu'il n'y a pas d'intensité rentrante (ce qui en revanche est vrai en général) on a
et
ce qui signifie que
Équation de transfert
L'intensité se conserve dans le vide
Si un rayonnement se propage dans le vide sans interagir avec la matière, son intensité reste constante.
Considérons en effet un ensemble de rayons lumineux traversant à la fois deux surfaces dS1 et dS2 situées à la distance r l'une de l'autre. Soit I1 l'intensité du faisceau lumineux au point 1. L'énergie traversant la première surface dS1 par unité de temps et de fréquence est, d'après la définition précédente
Au point 2 on écrirait de même
En comparant les deux expressions, on voit que
ce qui signifie que l'intensité d'un faisceau de lumière se propageant librement est la même en tout point du parcours.
Attention toutefois ! Cela ne signifie pas qu'à surface de réception donnée l'on captera la même quantité de lumière du Soleil quelle que soit la distance à laquelle on se place. Si l'intensité du rayonnement solaire est bien la même sur la Terre et sur la lointaine planète Neptune, située 20 fois plus loin de notre étoile centrale, l'angle solide (dS/r2) sous lequel le Soleil est vu de là-bas est 400 fois plus petit que de la Terre et par conséquent une surface donnée y recevra 400 fois moins d'énergie.
Absorption du rayonnement
Quand le rayonnement traverse un milieu contenant des particules (atomes neutres ou ionisés, électrons, molécules, grains, etc.), cette matière est susceptible d'absorber ou d'émettre de l'énergie lumineuse. On caractérise la capacité d'absorption du milieu par son coefficient d'absorption κ ν, qui a la dimension de l'inverse d'une longueur (et se mesure donc couramment en cm-1) et est défini de telle sorte que la quantité sans dimension (κ ν ds) représente la fraction de rayonnement absorbée le long du trajet ds. Cette quantité définit l'épaisseur optique de la couche infinitésimale selon la formule
Si une intensité I ν est absorbée le long du trajet sans qu'aucune émission n'intervienne, cette intensité est atténuée selon la loi
qui s'intègre pour donner la loi d'extinction
où
et (I ν)0 est l'intensité au point choisi comme origine s = 0.
On a supposé pour écrire ces expressions que le rayonnement ne change pas avec le temps.
Remarque : si on prend la longueur d'onde au lieu de la fréquence comme variable, comme κ ν est relatif à une fréquence et non à un intervalle de fréquence, on aura
quantité qui a toujours la dimension de l'inverse d'une longueur (et s'exprime donc en cm-1).
L'équation de transfert du rayonnement
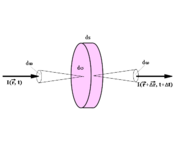
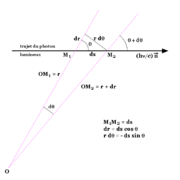
L'équation de transfert du rayonnement établit le bilan d'énergie dans le passage de photons de classe A à travers une surface dσ sur une longueur ds (voir la figure).
D'après la définition du coefficient d'absorption la partie d'énergie absorbée dans le faisceau est
- partie absorbée =
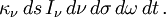
Pour calculer la partie émise par le volume traversé, on introduit un coefficient d'émission ε ν tel que l'énergie lumineuse de photons de classe A émise par le volume dV s'écrive sous la forme
- partie émise=
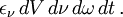
On voit que ε ν est une énergie par unité de fréquence par unité de volume par unité d'angle solide par unité de temps et s'exprime donc en erg·cm-3·s-1·sr-1·Hz-1.
À l'aide de ces définitions le bilan d'énergie des photons de classe A ayant traversé le volume élémentaire dσ ds s'écrit sous la forme
En se limitant au problème stationnaire, Iν est indépendant du temps et on a
de sorte que l'on obtient l'équation de transfert du rayonnement sous la forme :
Fonction source du rayonnement
En divisant par κν l'équation de transfert s'écrit encore
où la quantité
rapport du coefficient d'émission au coefficient d'absorption est appelée la fonction source. On voit que cette quantité a les dimensions d'une intensité et s'exprime donc dans les mêmes unités. À l'équilibre thermodynamique la fonction source est égale à la fonction de Planck
Cette équation différentielle s'intègre le long de la direction d'un faisceau lumineux sous la forme :
où
est l'épaisseur optique entre le point s' et le point s.
L'interprétation physique de cette formule est claire. Le premier terme représente l'intensité de rayonnement initial affaiblie par l'absorption sur le parcours de 0 à s. Le second représente les émissions ajoutées des différents points s’ dont la contribution est affaiblie par l'absorption entre le point d'émission s’ et le point s où l'on calcule l'intensité.
Géométrie sphérique
Les modèles d'étoiles les plus simples font l'hypothèse que ces objets possèdent la symétrie sphérique, c'est-à-dire qu'ils sont constitués d'un empilement de couches sphériques individuellement homogènes. Les quantités physiques, dont l'intensité du rayonnement en un point, ne dépendent alors spatialement parlant que de la variable r, distance du point au centre de l'étoile. Dans ce modèle l'intensité est une fonction du point choisi et de l'angle θ compris entre 0 et π donnant la direction du faisceau lumineux par rapport au rayon. Formellement :
Le schéma ci-contre indique la géométrie utilisée et permet d'écrire l'équation de transfert.
La dérivée de l'intensité le long du trajet du photon est :
Comme on le voit sur la figure on a les relations
de sorte que l'équation de transfert devient
Intégrons cette équation sur l'angle solide
Le deuxième terme de gauche de l'équation conduit à une intégrale qui peut s'intégrer par parties comme :
où H ν est le flux défini plus haut.
Le membre de gauche de l'équation de transfert intégré sur tout l'angle solide donne donc
L'équation de transfert complète intégrée sur tout l'angle solide s'écrit donc
où Jν est l'intensité moyenne du rayonnement.
Si l'équilibre radiatif est réalisé cela signifie par définition qu'en intégrant sur toutes les fréquences l'énergie absorbée est égale à l'énergie émise. On a donc
En considérant alors le membre de gauche on obtient le résultat
dans lequel C est une constante, indiquant que le flux par unité de surface varie comme l'inverse du carré du rayon de la couche traversée. Physiquement cela signifie que le flux total (4π r2 H ) franchissant les couches de l'étoile reste constant, ce qui est normal si ces dernières ne contiennent aucune source d'énergie.
Géométrie plan-parallèle
On utilise très souvent l'approximation dite « plan-parallèle » dans laquelle la courbure des couches de l'étoile est négligée. Cette approximation est valable si la largeur géométrique des couches considérées est petite devant la distance de ces couches au centre de l'étoile. Elle n'est pas valable pour des atmosphères étendues, un terme qui désigne les couches extérieures très diluées d'étoiles de grande taille, comme les géantes ou les supergéantes. Dans les équations du cas sphérique, il suffit de faire tendre r vers l'infini pour tomber sur l'équation de transfert plan-parallèle suivante :
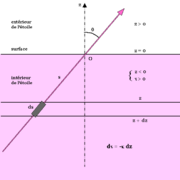
En définissant la profondeur optique τν le long de la normale aux couches selon les conventions précisées sur la figure par
(τ est nul pour z infini, c'est-à-dire à l'observateur) et en notant à nouveau
on obtient l'équation de transfert sous la forme usuelle
Il est utile à la fois du point de vue numérique et physique de distinguer entre intensité émergente I + et intensité entrante I -. Avec cette convention l'angle θ entre la normale à la couche et le rayon lumineux varie seulement entre 0 et π/2 et μ reste positif entre 0 et 1. On écrit
En introduisant les nouvelles variables u et v définies par
qui ont respectivement le caractère d'une intensité moyenne et d'un flux, on obtient le système :
C'est sur ce système d'équations que se basent toutes les méthodes différentielles de résolution numérique du transfert car, étant physiquement pertinent, il se révèle plus stable que l'équation de transfert sur I.
À la surface de l'étoile le rayonnement émergent suivant l'angle θ donné par son cosinus μ = cosθ s'exprime sous la forme :
Cette formule a un caractère très général. Elle permet de calculer directement l'intensité sortant d'une étoile si on connaît la fonction source du rayonnement en tout point de son atmosphère.
Approximations
Équilibre thermodynamique local
Une approximation utilisée très souvent en astrophysique est celle de l’équilibre thermodynamique local (ETL en français, LTE en anglais). Elle consiste à supposer que la fonction source du rayonnement est égale à la fonction de Planck, soit
Cette hypothèse revient à supposer que les populations des différents niveaux des atomes susceptibles d'émettre le rayonnement suivent la loi de Boltzmann, autrement dit que les atomes sont peuplés comme si l'équilibre thermodynamique régnait. Toute la subtilité du transfert réside en ce que si la fonction source est égale à la fonction de Planck, on ne peut pas en dire autant de l'intensité du rayonnement.
Approximations de diffusion
Les écarts à l'équilibre thermodynamique, qui se traduisent en particulier par le fait que l'intensité du rayonnement n'est pas égale à la fonction de Planck, sont intimement liés à la non-isotropie du rayonnement. Puisqu'un flux de lumière est transporté vers l'extérieur, c'est le signe que sur le bilan global l'intensité sortante doit être supérieure à l'intensité rentrante. L'équation de transfert nous permet de calculer cet effet. Pour fixer les idées nous nous placerons à l'ETL (équilibre thermodynamique local).
Dans les couches les plus profondes d'une étoile le rayonnement est emprisonné, se met de ce fait en équilibre avec la matière et devient lui aussi égal à la fonction de Planck. Mais cela n'est pas tout à fait vrai, autrement aucun rayonnement ne sortirait de l'étoile. L'approximation de diffusion consiste à développer la fonction source en fonction de la profondeur optique dans l'atmosphère autour du point τ ν selon la formule
L'intégration de l'équation de transfert fournit alors les résultats
Ne conserver dans ces expressions que les termes écrits revient à faire l'approximation de diffusion. Cette approximation a une grande importance historique car elle a permis de traiter des problèmes de transfert dans les atmosphères stellaires avant l'avènement de l'informatique. L’approximation d'Eddington est l'une des plus célèbres. Elle consiste à écrire que partout dans l'atmosphère
Dans ce que l'on appelle en astrophysique le cas gris, le coefficient d'absorption est pris comme constant sur les fréquences (ce qui n'est jamais réalisé d'ailleurs). On peut alors intégrer les équations précédentes sur les fréquences. Comme
où σ est la constante de Stefan-Boltzmann et T la température du corps noir. Il résulte de ce qui précède que dans l'approximation d'Eddington la quantité T 4 est une fonction linéaire de la profondeur optique τ, plus précisément
où T0 représente la température du gaz à la surface de l'étoile.
Relation de Barbier-Eddington
Supposons que la fonction source S soit une fonction linéaire
de la profondeur optique τ comptée le long de la ligne de visée. L'intégration de l'équation de transfert fournit pour l'intensité émergente de l'étoile la valeur
d'après des formules classiques.
En d'autres termes l'intensité I le long d'une ligne de visée est égale à la fonction source au point de cette ligne de visée situé à la distance optique unité. On résume rapidement ce fait en disant que l'intensité reflète la fonction source à la profondeur optique τ = 1. Ce résultat constitue l'approximation connue sous le nom de relation de Barbier-Eddington, une relation utilisée très souvent pour raisonner en ordre de grandeur.
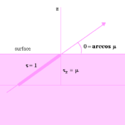
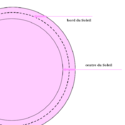
Si on se place en un point de la surface, il est facile de réaliser (figure ci-contre) que puisque l'on « voit » à τ = 1 on sonde dans la direction radiale des couches plus profondes que dans les directions tangentielles, cela à cause du facteur μ = cosθ reliant profondeur radiale et profondeur le long de la ligne de visée. Plus précisément dans la direction θ = arccosμ on « voit » la profondeur
Au bord d'une étoile, comme par exemple le Soleil, on voit donc des couches plus superficielles qu'au centre. Si la température décroît vers l'extérieur, ce qui est la situation la plus générale (et en tout cas ce que prévoient tous les modèles ETL), le bord apparaîtra plus sombre que le centre. Ainsi s'explique le phénomène de l'assombrissement centre-bord sur le disque solaire.
Température effective d'une étoile
En résumé, la température effective d'une étoile est la quantité Teff telle que l'énergie totale par unité de temps émise par l'astre s'exprime sous la forme
où R est le rayon de l'étoile supposée sphérique. Autrement dit, par définition
La quantité E se mesure en erg/s dans le système CGS ou en watt en unités SI.
Comme application numérique calculons la température effective du Soleil. Cet astre émet une luminosité totale
et son rayon est
Avec σ = 5,67×10-8 W⋅m-2⋅K -4 on trouve
La température effective d'une étoile est un paramètre servant à mesurer la quantité totale d'énergie lumineuse émise par cet astre. On la définit comme la température du corps noir qui émettrait dans l'espace la même quantité d'énergie. Comme une étoile ne rayonne pas comme un corps noir, cette quantité n'est pas une « vraie » température. Elle a néanmoins un certain rapport avec la température des couches superficielles de l'étoile.
Considérons un corps noir de température T. Un tel corps noir émet une intensité de lumière I indépendante de la direction égale à la fonction de Planck, soit :
D'après la définition de l'intensité I ν le flux à la fréquence ν émergeant d'une ouverture de surface unité faite dans la cavité du corps noir est
Le flux total émis est donc
où σ est la constante de Stefan-Boltzmann. En sens inverse, à flux donné, la température donnée par cette relation sera par définition la température effective de l'étoile. Pour obtenir le flux total émis par toute l'étoile, on intègrera encore cette quantité sur toute sa surface.
Calculons maintenant directement le flux en intégrant l'équation de transfert. Dans le cadre de l'approximation d'Eddington, la fonction source du rayonnement est donnée en fonction de la profondeur optique par la fonction linéaire
L'intensité émergente à la fréquence ν dans la direction arccosμ est égale à
Le flux traversant une surface unité est
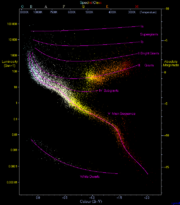 Diagramme de Hertzsprung-Russell créé par Richard Powell et diffusé sur Wikipédia avec sa permission. La luminosité totale d'une étoile est portée en fonction de la température effective de sorte que sur une même verticale l'ordonnée d'un point mesure la surface de l'étoile.
Diagramme de Hertzsprung-Russell créé par Richard Powell et diffusé sur Wikipédia avec sa permission. La luminosité totale d'une étoile est portée en fonction de la température effective de sorte que sur une même verticale l'ordonnée d'un point mesure la surface de l'étoile.
Si on fait de plus l'hypothèse de l'ETL, la fonction source S0(ν) à la surface est égale à la fonction de Planck Bν(T0) à la température T0 de surface (qui maintenant, dans le cadre de l'hypothèse de l'équilibre thermodynamique local, est une « vraie » température), de sorte que l'on obtient en intégrant sur les fréquences
En comparant les deux expressions du flux à travers une surface unité, on voit que
et par conséquent
Par comparaison la résolution exacte du cas gris donne
ce qui montre que l'approximation d'Eddington est assez exacte (au moins dans certaines circonstances). On voit que le paramètre de température effective est assez voisin de la température du gaz de surface et possède de ce fait une certaine signification physique (surtout si on se contente d'ordres de grandeur) mais cela n'implique pas que le rayonnement émergent lui-même suive la loi de Planck.
Pour reconnaître une étoile dans le ciel et en déduire ses paramètres physiques, les astronomes utilisent sa température effective et sa luminosité totale. Lorsque l'on porte les étoiles dans un diagramme basé sur ces deux paramètres (le justement célèbre diagramme de Hertzsprung-Russell, ou « diagramme HR »), les points ne se répartissent pas au hasard mais selon des séquences définies (comme la séquence principale). L'analyse de la structure de ce diagramme a permis d'établir la théorie de l'évolution d'une étoile. Les points ayant même abscisse dans ce diagramme ont même température effective et par conséquent, par définition de cette température effective, même énergie lumineuse émise par unité de surface. Il en résulte que l'ordonnée du point représentatif d'une étoile sur une même verticale est une simple mesure du carré du rayon de l'astre. Les étoiles les plus grosses (géantes ou supergéantes) sont situées dans le haut du diagramme et les plus petites (naines), dans la partie basse.
Annexes
Bibliographie
- Guy Moreels (coordonné par), Interaction rayonnement-matière dans les atmosphères planétaires et cométaires, Ellipses Marketing, 2001 (ISBN 978-2729879549)
- Richard Monier, Les étoiles et le milieu interstellaire : Introduction à l'astrophysique, Ellipses Marketing, 2006 (ISBN 978-2729827861)
- Ouvrages spécialisés en anglais
- Subrahmanyan Chandrasekhar (1960) Radiative transfer, éd New York: Dover, (ISBN 0486-6059-06)
- Dimitri Mihalas (1970) Stellar atmospheres, éd. W. H. Freeman and company, (ISBN 0716-7033-35)
Notes et références
- ↑ C'est la raison pour laquelle le ciel est bleu.
Articles connexes
- Portail de l’astronomie
- Portail de la physique
Catégories : Astrophysique | Physique stellaire | Électromagnétisme
Wikimedia Foundation. 2010.

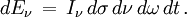
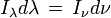
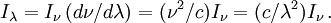
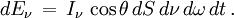
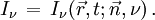
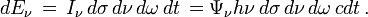
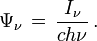
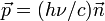
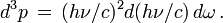
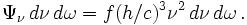
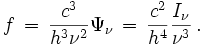
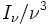
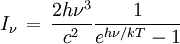
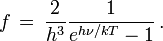
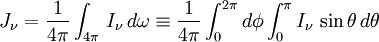
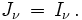
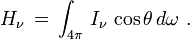
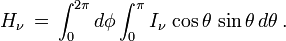
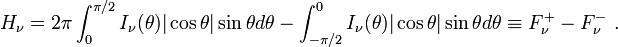
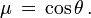
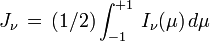
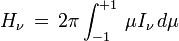
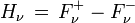
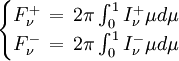
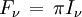
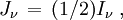
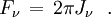

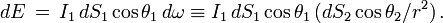
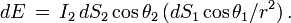
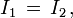
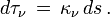
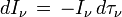
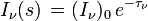
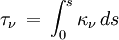
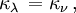
![[I_\nu(\vec{r}+\Delta\vec{r}, \,t+\Delta t) -I_\nu(\vec{r},\,t)]\,d\sigma d\omega d\nu dt = (\epsilon_\nu - \kappa_\nu I_\nu)\,d\sigma ds d\nu d\omega dt\,.](/pictures/frwiki/53/545bec7c15804718fa3578051aa5854b.png)
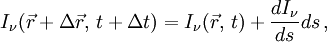
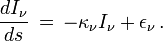
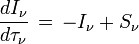
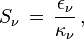
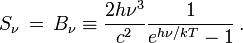
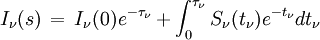
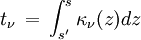
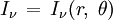
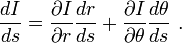
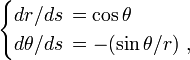
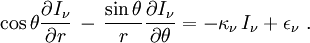
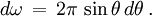
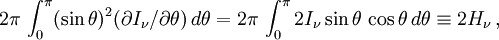
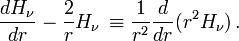
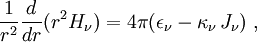
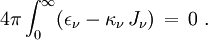
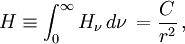
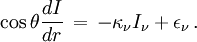
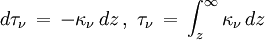
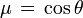
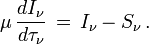
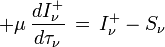
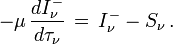
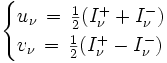
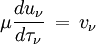
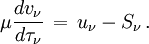
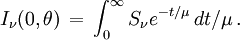
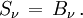
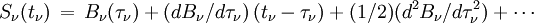
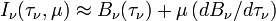
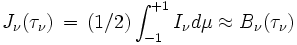
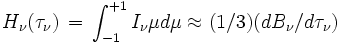
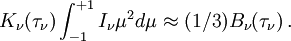
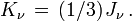
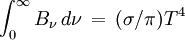
![T^{\,4} \,=\,T_0^{\,4}\, [1 + (3/2)\tau]](/pictures/frwiki/57/99a85ef091f766b67fa4acba296083d6.png)
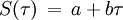
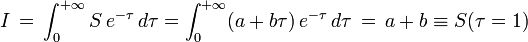
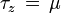
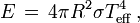
![T_{\rm eff}\,=\,[E/(4\pi R^2\sigma)]^{1/4}\,.](/pictures/frwiki/48/0debbd8bb77f9b2c508b1814e0a8fa8e.png)
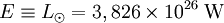
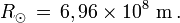
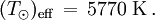
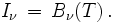
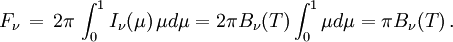
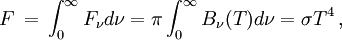
![S(\nu, \,\tau_\nu)\,=\,S_0(\nu)\,[1+(3/2)\tau_\nu]\,.](/pictures/frwiki/53/5ab011d5979747646b68498cd17168c5.png)
![I_\nu (\mu) \,=\,\int_0^\infty S(\nu, t) e^{-t/\mu}\,dt/\mu = \int_0^\infty S_0(\nu)[1+(3/2)t]\, e^{-t/\mu}\,dt/\mu= S_0(\nu)[1 + (3/2)\mu]\,.](/pictures/frwiki/57/9b586d36cb70e6991cf12bb8d4c9be26.png)
![F_\nu \,=\, 2\pi\int_0^\infty S_0(\nu) [1 + (3/2)\mu] \,\mu d\mu = 2 \pi S_0 (\nu)\,.](/pictures/frwiki/52/4623c6a59712dd265095e3e4ff7fb8a3.png)