- Instabilité de Rayleigh–Taylor
-
Instabilité de Rayleigh-Taylor
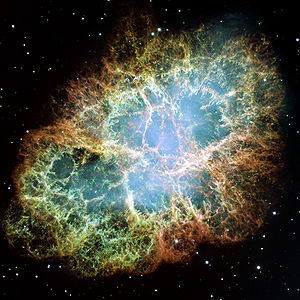 Manifestation de l'instabilité de Rayleigh–Taylor dans la nébuleuse du Crabe.
Manifestation de l'instabilité de Rayleigh–Taylor dans la nébuleuse du Crabe.
L’instabilité de Rayleigh–Taylor, nommée en hommage aux physiciens britanniques Lord Rayleigh et G. I. Taylor, est une instabilité de l’interface séparant deux fluides de densités différentes, qui résulte de la poussée du fluide le plus lourd sur le fluide le plus léger (l'accélération dans le cas d'un système dynamique ou la gravité pour un système initialement statique est dirigée vers la phase légère)[1],[2]. Ce phénomène est produit par exemple par l'onde de choc à l'origine des nuages interstellaires. Dans ce cas particulier où le choc est à l'origine de la mise en vitesse du système, on parlera d'instabilité de Richtmyer-Meshkov. Il se produit une situation analogue lorsque la gravité affecte deux fluides de densités différentes (le fluide le plus dense se trouvant au dessus du fluide le moins dense) comme de l'huile minérale à la surface de l'eau[2].
Considérons deux couches de fluides immiscibles superposées dans deux plans parallèles, la plus lourde surplombant la plus légère et toutes deux soumises à la pesanteur terrestre. L’équilibre est instable à la moindre perturbation : toute perturbation va s'amplifier et libérer de l’énergie potentielle, le fluide le plus lourd gagnant progressivement la moitié inférieure sous l'effet du champ de gravitation, et le fluide léger passe au-dessus. C'est cette configuration qu'a étudiée Lord Rayleigh[2]. La découverte importante de G. I. Taylor a consisté à montrer que cette situation est équivalente à celle qui se produit lorsque les fluides (hors de toute gravité) sont accélérés, le fluide léger étant propulsé à l'intérieur du fluide le plus lourd[2]. Cela se produit notamment lorsque l'on projette un verre à terre avec une accélération supérieure à la pesanteur terrestre[2] g.
Lorsque l’instabilité développe ses effets, des irrégularités (« fossettes ») se propagent vers le bas en polypes de Rayleigh–Taylor qui finissent même par se mélanger. C'est pourquoi on qualifie parfois l’instabilité de Rayleigh–Taylor d’instabilité à traines (fingering instability)[3]. Le fluide le plus léger s'expand vers le haut comme un champignon nucléaire[4],[5].
On observe ce phénomène dans plusieurs situations courantes, non seulement dans les dômes salins ou les couches d’inversion, mais aussi en astrophysique et en électrocinétique. Les polypes de Rayleigh-Taylor sont particulièrement visibles dans la Nébuleuse du Crabe, où le plérion engendré par le pulsar du Crabe déborde les projections issues de l’explosion de la supernova il y a 1 000 ans[6].
Il ne faut pas confondre l’instabilité de Rayleigh–Taylor avec l’instabilité de Plateau-Rayleigh (parfois appelée « instabilité du tuyau d'arrosage ») : cette dernière, qui se produit dans les jets de liquide, est due à la tension superficielle, qui tend à disperser un jet cylindrique en une projection de gouttelettes de même volume mais de surface spécifique moindre.
Sommaire
Analyse linéaire de la stabilité
Fichier:Rti base.pngConfiguration de base state de l’instabilité de Rayleigh–Taylor. La gravité est tournée vers le bas.L’instabilité bidimensionnelle non-visqueuse de Rayleigh–Taylor constitue un excellent banc d'essai pour l'étude mathématique de la stabilité du fait de la nature extrêmement simple de la configuration initiale[7], décrite par un champ de vitesse moyenne tel que
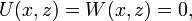 où le champ gravitationnel est
où le champ gravitationnel est 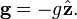 Une interface en
Une interface en 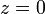 sépare les fluides de densités
sépare les fluides de densités 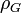 dans la zone supérieure, et
dans la zone supérieure, et 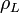 dans la zone inférieure. On montre que dans cette section, lorsque le fluide le plus lourd se trouve au-dessus, la moindre perturbation de l’interface s’amplifie exponentiellement, avec le taux[2]
dans la zone inférieure. On montre que dans cette section, lorsque le fluide le plus lourd se trouve au-dessus, la moindre perturbation de l’interface s’amplifie exponentiellement, avec le taux[2]où
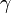 est le taux de croissance,
est le taux de croissance, 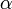 est le nombre d'onde spatial et
est le nombre d'onde spatial et 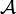 est le Nombre d'Atwood.
est le Nombre d'Atwood.La perturbation apportée au système est décrite par un champ de vitesse d'amplitude infiniment petite,
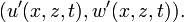 Comme on suppose le fluide incompressible, ce champ de vitesse est irrotationel et peut être décrit par des lignes de courant.
Comme on suppose le fluide incompressible, ce champ de vitesse est irrotationel et peut être décrit par des lignes de courant.où les indices indiquent les dérivations partielles. En outre, dans un fluide incompressible initialement en mouvement stationnaire, il n'y a pas de tourbillon, et le champ de vitesse du fluide demeure irrotationnel, soit
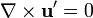 . En termes de ligne de courant,
. En termes de ligne de courant, 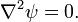 Ensuite, comme le système est invariant par toute translation dans la direction x, on peut chercher une solution sous la forme
Ensuite, comme le système est invariant par toute translation dans la direction x, on peut chercher une solution sous la formeoù
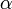 est le nombre d'onde spatial. Ainsi, le problème se ramène à la résolution de l'équation
est le nombre d'onde spatial. Ainsi, le problème se ramène à la résolution de l'équationLe domaine sur lequel on résout le problème est le suivant : le fluide indexé « L » est confiné à la région
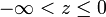 , tandis que le fluide indexé « G » se trouve dans le demi-plan supérieur
, tandis que le fluide indexé « G » se trouve dans le demi-plan supérieur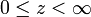 . Pour la détermination de la solution complète, il faut fixer les conditions aux limites et à l’interface. Cela détermine la célérité c, laquelle à son tour gouverne les propriétés de stabilité du système.
. Pour la détermination de la solution complète, il faut fixer les conditions aux limites et à l’interface. Cela détermine la célérité c, laquelle à son tour gouverne les propriétés de stabilité du système.La première de ces conditions est fournie par les données aux limites. Les vitesses de perturbation
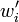 devraient satisfaire une condition d'imperméabilité (flux nul), interdisant au fluide de s'expandre en dehors du domaine d'étude
devraient satisfaire une condition d'imperméabilité (flux nul), interdisant au fluide de s'expandre en dehors du domaine d'étude 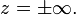 Ainsi,
Ainsi, 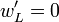 le long de
le long de 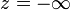 , et
, et 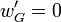 pour
pour 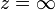 . En termes de lignes de courant, cela s'écrit
. En termes de lignes de courant, cela s'écritLes trois autres conditions sont fournies par le comportement de l’interface
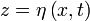 .
.Continuité de la composante verticale de vitesse ; en z = η, les composantes verticales de vitesse doivent se raccorder :
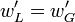 . En termes de lignes de courant, cela s'écrit
. En termes de lignes de courant, cela s'écritPar un développement limité en
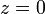 on obtient
on obtientC’est l’équation exprimant la condition d’interface.
Condition de surface libre : Le long de la surface libre
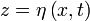 , la condition condition cinématique suivante s'applique:
, la condition condition cinématique suivante s'applique:Par linéarisation, on obtient simplement
où la vitesse
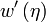 est linéarisée sur la surface
est linéarisée sur la surface 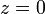 . En utilisant les représentations de mode normal et les lignes de courant, cette condition est
. En utilisant les représentations de mode normal et les lignes de courant, cette condition est  , deuxième condition d’interface.
, deuxième condition d’interface.Saut de pression à l'interface: Dans le cas où l'on prend en compte une tension superficielle, le saut de pression à travers l’interface en z = η est donné par l’équation de Laplace :
où σ est la tension superficielle et κ est la courbure de l’interface, dont une approximation s'obtient en linéarisant :
Ainsi,
Toutefois, cette condition fait intervenir la pression totale (=pression de base+perturbation), c'est-à-dire
(Comme d'habitude, on peut linéariser les perturbations des différentes grandeurs le long de la surface z=0.) En exprimant l’équilibre hydrostatique, sous la forme
on obtient
L’altération du champ de pression est évaluée par les fonctions de courant, grâce à l’équation de l'impulsion horizontale tirée des équations d'Euler linéarisées pour les perturbations,
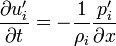 avec
avec 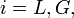 qui donne
qui donneReportant cette dernière équation avec la condition de saut,
En exploitant la deuxième condition d'interface
 et en utilisant la représentation de mode normal, cette relation devient
et en utilisant la représentation de mode normal, cette relation devientoù il est d'ailleurs inutile d'indexer
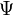 (seulement ses dérivées) puisque
(seulement ses dérivées) puisque 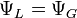 lorsque
lorsque 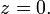
Solution
À présent qu'on a décrit mathématiquement le modèle d'écoulement stratifié, la solution est à portée. L’équation des lignes de courant
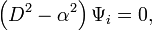 avec les conditions aux limites
avec les conditions aux limites 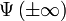 se résout selon
se résout selonLa première condition d’interface édicte que
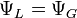 en
en 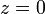 , ce qui impose
, ce qui impose 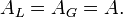 La troisième condition d’interface édicte que
La troisième condition d’interface édicte queReportant la solution dans cette équation, on forme la relation
Le A se simplifie de part et d'autre, et il reste
Pour interpréter complètement ce résultat, il est intéressant de considérer le cas où la tension superficielle est nulle. Dans ce cas,
et il est ainsi clair que
- si
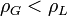 ,
, 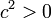 et c est réel. C’est ce qui advient quand le fluide le plus léger est au dessus;
et c est réel. C’est ce qui advient quand le fluide le plus léger est au dessus; - si
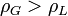 ,
, 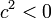 et c est imaginaire pur : c’est ce qui advient quand le fluide le plus lourd est au dessus.
et c est imaginaire pur : c’est ce qui advient quand le fluide le plus lourd est au dessus.
Donc, lorsque le fluide le plus lourd est au dessus,
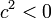 , et
, etoù
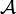 est le Nombre d'Atwood. En ne considérant que la solution positive, nous voyons que la solution est de la forme
est le Nombre d'Atwood. En ne considérant que la solution positive, nous voyons que la solution est de la formeet qu'elle est associée à la position η de l’interface par :
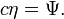 Posons à présent
Posons à présent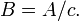
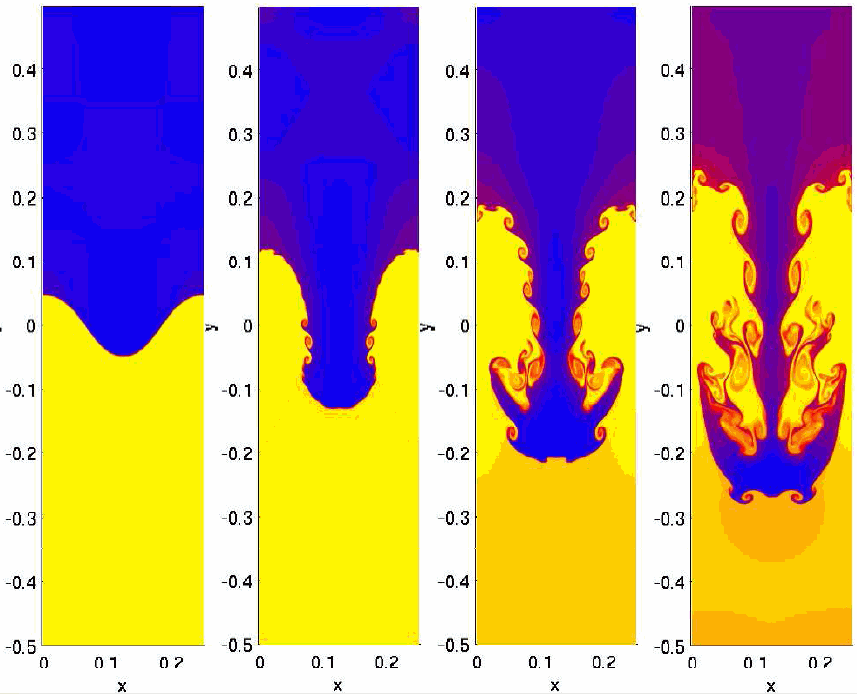 Simulation hydrodynamique d’un « polype » isolé de l’instabilité de Rayleigh–Taylor[9]. Observez la formation d'une instabilité de Kelvin-Helmholtz, à partir de la deuxième image (se développant à partir du niveau y = 0), ainsi que la formation d’un chapeau de champignon à un stade évolué dans les troisième et quatrième images de cette séquence.
Simulation hydrodynamique d’un « polype » isolé de l’instabilité de Rayleigh–Taylor[9]. Observez la formation d'une instabilité de Kelvin-Helmholtz, à partir de la deuxième image (se développant à partir du niveau y = 0), ainsi que la formation d’un chapeau de champignon à un stade évolué dans les troisième et quatrième images de cette séquence.
Le temps caractéristique de croissance de la surface libre
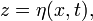 initialement en
initialement en 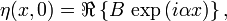 est donné par :
est donné par :qui croît exponentiellement avec le temps. Ici B désigne l’amplitude de la perturbation initiale, et
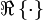 est la partie réelle de l’expression complexe entre parenthèses.
est la partie réelle de l’expression complexe entre parenthèses.En général, la condition pour que l’instabilité soit linéaire est que la partie imaginaire de la célérité complexe c soit positive. Finalement, le rétablissement de la tension superficielle diminue c2 en module et a donc un effet stabilisant. En effet, il existe un domaine d'ondes courtes pour lesquelles la tension superficielle stabilise le système et empêche l’instabilité.
Comportement à long terme
L’analyse qui précède n'est plus valable quand on a affaire à une perturbation de grande amplitude : dans ce cas, la croissance est non-linéaire, les polypes et les bulles s'entrelacent et s'enroulent en tourbillons. Comme l'illustre la figure ci-contre, il faut recourir à la simulation numérique[10], pour décrire mathématiquement le système.
Notes et références
- ↑ D.H. Sharp, « An Overview of Rayleigh-Taylor Instability », dans Physica D, vol. 12, 1984, p. 3–18 [lien DOI]
- ↑ a , b , c , d , e et f Drazin (2002) pp. 50–51.
- ↑ « The Rayleigh–Taylor instability in the spherical pinch », dans Journal of Fusion Energy, vol. 13, no 4, 1994, p. 275–280 [lien DOI]
- ↑ Modèle:Cite arxiv
- ↑ R. J. Tayler (dir.), W. Hillebrandt et P. Höflich, Stellar Astrophysics, Supernova 1987a in the Large Magellanic Cloud, CRC Press, 1992 (ISBN O750302003), p. 249–302 : cf. page 274.
- ↑ J. Jeff Hester, « The Crab Nebula: an Astrophysical Chimera », dans Annual Review of Astronomy and Astrophysics, vol. 46, 2008, p. 127–155 [lien DOI]
- ↑ a et b Drazin (2002) pp. 48–52.
- ↑ On trouve un calcul similaire dans l'ouvrage de Chandrasekhar (1981), §92, pp. 433–435.
- ↑ Shengtai Li et Hui Li, « Parallel AMR Code for Compressible MHD or HD Equations », Los Alamos National Laboratory. Consulté le 2006-09-05
- ↑ IUSTI, « Simulation numérique des instabilités de Richtmyer-Meshkov ». Mis en ligne le 6 octobre 2008, consulté le 20 août 2009
Voir aussi
- Instabilité de Richtmyer-Meshkov
- Instabilité de Kelvin-Helmholtz
- Champignon nucléaire
- Instabilité de Plateau-Rayleigh
- Stabilité hydrodynamique
- Allée de tourbillons de Karman
Bibliographie
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Rayleigh-Taylor Instability ».
Sources historiques
- John William Strutt Rayleigh, « Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density », dans Proceedings of the London Mathematical Society, vol. 14, 1883, p. 170–177 [lien DOI] (Original paper is available at: https://www.irphe.univ-mrs.fr/~clanet/otherpaperfile/articles/Rayleigh/rayleigh1883.pdf .)
- Geoffrey Ingram Taylor, « The instability of liquid surfaces when accelerated in a direction perpendicular to their planes », dans Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, vol. 201, no 1065, 1950, p. 192–196 [lien DOI]
Bibliographie récente
- Subrahmanyan Chandrasekhar, Hydrodynamic and Hydromagnetic Stability, Dover Publications, 1981 (ISBN 978-0486640716)
- P. G. Drazin, Introduction to hydrodynamic stability, Cambridge University Press, 2002, xvii+238 pages p. (ISBN 0-521-00965 0) .
- P. G. Drazin et W. H. Reid, Hydrodynamic stability, Cambridge University Press, Cambridge, 2004 (réimpr. 2nd), 626 p. (ISBN 0-521-52541-1)
Liens externes
- Démonstration Java de l’instabilité RT dans les fluides
- Véritables images et vidéos d’allées RT
- Expériences sur l'instabilité Rayleigh-Taylor à l’Université d’Arizona
- Portail de la physique
Catégories : Mécanique des fluides | Transfert thermique | Thermodynamique atmosphérique
Wikimedia Foundation. 2010.

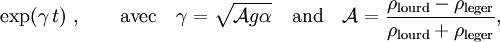
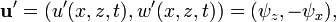
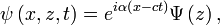
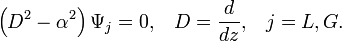

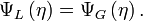
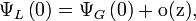
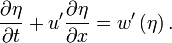
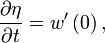
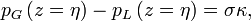
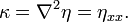
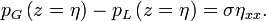
![\left[P_G\left(\eta\right)+p'_G\left(0\right)\right]-\left[P_L\left(\eta\right)+p'_L\left(0\right)\right]=\sigma\eta_{xx}.\,](/pictures/frwiki/102/f80d4844b332a7028aecdc125f028475.png)

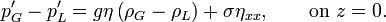
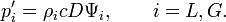
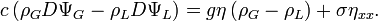
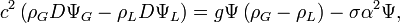

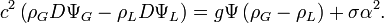
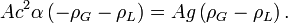
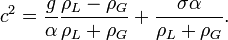
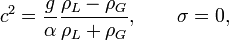
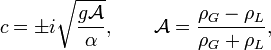
![\Psi\left(x,z,t\right)=Ae^{-\alpha|z|}\exp\left[i\alpha\left(x-ct\right)\right]=A\exp\left(\alpha\sqrt{\frac{g\tilde{\mathcal{A}}}{\alpha}}t\right)\exp\left(i\alpha
x-\alpha|z|\right)\,](/pictures/frwiki/102/fe041d7704ca1ccf22fb1d9d59858576.png)
