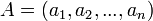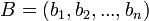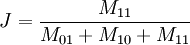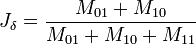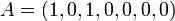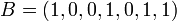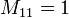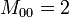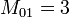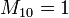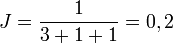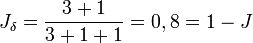Index et distance de Jaccard

Index et distance de Jaccard

Indice et distance de Jaccard

L'indice et la distance de Jaccard sont deux métriques utilisées en statistiques pour comparer la similarité et la diversité entre des échantillons. Elles sont nommées d'après le botaniste suisse Paul Jaccard.

Sommaire

Description formelle

L'indice de Jaccard (ou coefficient de Jaccard) est le rapport entre la cardinalité (la taille) de l'intersection des ensembles considérés et la cardinalité de l'union des ensembles. Il permet d'évaluer la similarité entre les ensembles. Soit deux ensembles A et B, l'indice est :

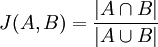J(A,B) = \frac{|A \cap B|}{|A \cup B|}.

L'extension à n ensembles est triviale :

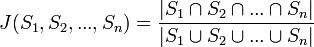J(S_1, S_2, ..., S_n) = \frac{|S_1 \cap S_2 \cap ... \cap S_n |}{|S_1 \cup S_2 \cup ... \cup S_n |}.

La distance de Jaccard mesure la dissimilarité entre les ensembles. Elle consiste simplement à soustraire l'indice de Jaccard à 1.

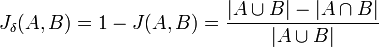J_{\delta}(A,B) = 1 - J(A,B) = { { |A \cup B| - |A \cap B| } \over |A \cup B| }.

De la même manière que pour l'indice, la généralisation devient :

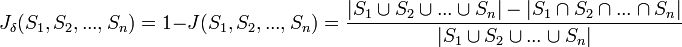J_{\delta}(S_1, S_2, ..., S_n) = 1 - J(S_1, S_2, ..., S_n) = \frac{|S_1 \cup S_2 \cup ... \cup S_n | - |S_1 \cap S_2 \cap ... \cap S_n |}{|S_1 \cup S_2 \cup ... \cup S_n |}.

Similarité entre des ensembles binaires

L'indice de Jaccard est utile pour étudier la similarité entre des objets constitués d'attributs binaires.

Soit deux séquences A et B, chacune avec n attributs binaires. Chaque attribut peut être à 0 ou 1. On a ainsi :

A = (a_1, a_2, ..., a_n)~
B = (b_1, b_2, ..., b_n)~

On définit plusieurs quantités qui caractérisent les deux ensembles :

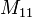M_{11}~ représente le nombre d'attributs qui valent 1 dans A et dans B
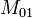M_{01}~ représente le nombre d'attributs qui valent 0 dans A et 1 dans B
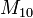M_{10}~ représente le nombre d'attributs qui valent 1 dans A et 0 dans B
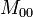M_{00}~ représente le nombre d'attributs qui valent 0 dans A et dans B

Chaque paire d'attributs doit nécessairement appartenir à l'une des quatre catégories, de telle sorte que :

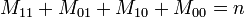M_{11} + M_{01} + M_{10} + M_{00} = n ~.

L'indice de Jaccard devient :

J = {M_{11} \over M_{01} + M_{10} + M_{11}}

La distance de Jaccard devient:

J_{\delta} = {M_{01} + M_{10} \over M_{01} + M_{10} + M_{11}}

Exemple

A = (1,0,1,0,0,0,0)~
B = (1,0,0,1,0,1,1)~
M_{11} = 1 ~
M_{00} = 2 ~
M_{01} = 3 ~
M_{10} = 1 ~
J = \frac{1}{ 3 + 1 + 1} = 0,2
J_{\delta} = \frac{3+1}{ 3 + 1 + 1} = 0,8 = 1 - J

Voir aussi

Références

  • Pang-Ning Tan, Michael Steinbach and Vipin Kumar, Introduction to Data Mining (2005), ISBN 0-321-32136-7
  • Paul Jaccard (1901) Bulletin de la Société Vaudoise des Sciences Naturelles 37, 241-272.
  • Tanimoto, T.T. (1957) IBM Internal Report 17th Nov. 1957.

Liens externes

  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Indice et distance de Jaccard ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Index et distance de Jaccard de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Jaccard index — The Jaccard index, also known as the Jaccard similarity coefficient (originally coined coefficient de communauté by Paul Jaccard), is a statistic used for comparing the similarity and diversity of sample sets.The Jaccard coefficient measures… …   Wikipedia

  • Sørensen similarity index — The Sørensen index, also known as Sørensen’s similarity coefficient, is a statistic used for comparing the similarity of two samples. It was developed by the botanist Thorvald Sørensen and published in 1948 [Sørensen, T. (1948) A method of… …   Wikipedia

  • Levenshtein distance — In information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences. The term edit distance is often used to refer specifically to Levenshtein distance. The… …   Wikipedia

  • Hamming distance — 3 bit binary cube for finding Hamming distance …   Wikipedia

  • Dice's coefficient — Dice s coefficient, named after Lee Raymond Dice[1] and also known as the Dice coefficient, is a similarity measure over sets: It is identical to the Sørensen similarity index, and is occasionally referred to as the Sørensen Dice coefficient. It… …   Wikipedia

  • Glossaire du data mining — Exploration de données Articles principaux Exploration de données Fouille de données spatiales Fouille du web Fouille de flots de données Fouille de textes …   Wikipédia en Français

  • Indice de Tanimoto — Similarité cosinus La similarité cosinus (ou mesure cosinus) permet de calculer la similarité entre deux vecteurs à n dimensions en déterminant l angle entre eux. Cette métrique est fréquemment utilisée en fouille de textes. Soit deux vecteurs A… …   Wikipédia en Français

  • Similarite cosinus — Similarité cosinus La similarité cosinus (ou mesure cosinus) permet de calculer la similarité entre deux vecteurs à n dimensions en déterminant l angle entre eux. Cette métrique est fréquemment utilisée en fouille de textes. Soit deux vecteurs A… …   Wikipédia en Français

  • Similarité cosine — Similarité cosinus La similarité cosinus (ou mesure cosinus) permet de calculer la similarité entre deux vecteurs à n dimensions en déterminant l angle entre eux. Cette métrique est fréquemment utilisée en fouille de textes. Soit deux vecteurs A… …   Wikipédia en Français

  • Similarité cosinus — La similarité cosinus (ou mesure cosinus) permet de calculer la similarité entre deux vecteurs à n dimensions en déterminant l angle entre eux. Cette métrique est fréquemment utilisée en fouille de textes. Soit deux vecteurs A et B, l angle θ s… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”