- Similarite cosinus
-
Similarité cosinus
La similarité cosinus (ou mesure cosinus) permet de calculer la similarité entre deux vecteurs à n dimensions en déterminant l'angle entre eux. Cette métrique est fréquemment utilisée en fouille de textes.
Soit deux vecteurs A et B, l'angle θ s'obtient par le produit scalaire et la norme des vecteurs :
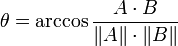 .
.
Comme l'angle θ est compris dans l'intervalle [0,π], la valeur π indiquera des vecteurs résolument opposés, π / 2 des vecteurs indépendants (orthogonaux) et 0 des vecteurs colinéaires. Les valeurs intermédiaires permettent d'évaluer le degré de similarité.
Dans le cas d'une comparaison de documents textuels
La similarité cosinus est fréquemment utilisée en tant que mesure de ressemblance entre deux documents. Il pourra s'agir de comparer les textes issus d'un corpus dans une optique de classification (regrouper tous les documents relatifs à une thématique particulière), ou de recherche d'information (dans ce cas l'un des documents vectorisé est constitué par les mots de la requête, et est comparés par mesure de cosinus de l'angle avec des vecteurs correspondants à tous les documents présents dans le corpus. On évalue ainsi lesquels sont les plus proches).
La mesure d'angle entre deux vecteurs ne pouvant être réalisée qu'avec des valeurs numériques, il faut imaginer un moyen de convertir les mots d'un document en nombres. On partira d'un index correspondant aux mots présents dans le documents puis on attribuera à ces mots des valeurs. La forme la plus simple pourrait être de compter le nombre d'occurrences des mots dans les documents.
En règle générale, pour mesurer finement la similarité entre des séquences de texte, les vecteurs sont construit d'après un calcul de type TF-IDF (term frequency–inverse document frequency) qui permet d'estimer l'importance d'un mot par rapport au document qui le contient, en tenant compte du poids de ce mot dans le corpus complet.
Indice de Tanimoto
L'indice de Tanimoto reprend cette idée dans le cas des attributs binaires. Il se définit comme suit :
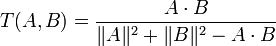 .
.
Voir aussi
- Portail des probabilités et des statistiques
Catégories : Traitement automatique du langage naturel | Analyse des données
Wikimedia Foundation. 2010.
