Algorithme De Floyd-Warshall

En informatique, l'algorithme de Floyd-Warshall (parfois appelé algorithme de Roy-Floyd car décrit par Bernard Roy en 1959) est un algorithme pour déterminer tous les plus courts chemins dans un graphe orienté et valué, en temps cubique.

Algorithme

L'algorithme de Floyd-Warshall prend en entrée un graphe orienté et valué (V, E), sous la forme d'une matrice d'adjacence donnant le poids d'un arc lorsqu'il existe et la valeur ∞ sinon. Le poids d'un chemin entre deux sommets est la somme des poids sur les arcs constituant ce chemin. Les arcs du graphe peuvent avoir des poids négatifs, mais le graphe ne doit pas posséder de cycle de poids strictement négatif. L'algorithme calcule, pour chaque paire de sommets, le poids minimal parmi tous les chemins entre ces deux sommets.

Soit V = {1, 2, 3, 4, ..., n} l'ensemble des sommets de G et soient i et j deux sommets de V. On considère un chemin p entre i et j de poids minimal dont les sommets intermédiaires sont dans {1, 2, 3, ..., k}. L'algorithme de Floyd-Warshall est basé sur l'observation suivante :

• soit p n'emprunte pas le sommet k ;
• soit p emprunte exactement une fois le sommet k (car les cycles sont de poids positifs ou nuls) et p est donc la concaténation de deux chemins, entre i et k et k et j respectivement, dont les sommets intermédiaires sont dans {1, 2, 3, ..., k-1}.

Notons 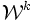la matrice telle que 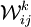est le poids minimal d'un chemin de i à j n'empruntant que des sommets intermédiaires dans {1, 2, 3, ..., k}, s'il en existe un, et ∞ sinon. 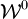est la matrice définissant G. L'observation ci-dessus se traduit par l'égalité 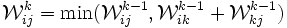, pour tous i, j et k dans {1, 2, 3, 4, ..., n}, en supposant les opérations min et + convenablement adaptées au cas d'un opérande ∞. Dès lors, on peut calculer successivement les matrices 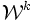pour k=1, 2, 3, 4, ..., n. Le calcul peut même être effectué en place, dans une unique matrice 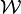. Le pseudo-code suivant effectue ce calcul :

procedure FloydWarshall (G : matrice )

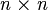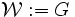for k: = 1 to n
    for i: = 1 to n
        for j: = 1 to n
            

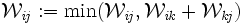
La complexité en temps de cet algorithme est O(n³) et sa complexité en espace O(n²).

Applications

L'algorithme de Floyd-Warshall peut être utilisé dans les situations suivantes :

• Plus courts chemins dans les graphes orientés (tous les arcs sont de poids 1)
• Clôture transitive d'un graphe orienté (algorithme de Warshall). Dans la formulation initiale de l'algorithme ci-dessus par Wharshall, le graphe n'est pas valué et donc simplement représenté par une matrice de booléens. On obtient alors la clôture transitive de ce graphe en remplaçant dans l'algorithme ci-dessus l'addition par la conjonction (ET) et le minimum par la disjonction (OU).
• Trouver une expression régulière dénotant le langage rationnel défini par un automate fini

Références

• (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7.
  • Section 26.2, "The Floyd-Warshall algorithm", pp. 558–565;
  • Section 26.4, "A general framework for solving path problems in directed graphs", pp. 570–576.
• (en) Robert W. Floyd, « Algorithm 97: Shortest Path », dans Communications of the ACM, vol. 5, n^o 6, June 1962, p. 345 
• (en) Stephen Warshall, « A theorem on Boolean matrices », dans Journal of the ACM, vol. 9, n^o 1, January 1962, p. 11–12 

Voir aussi

• Robert Floyd
• Algorithme de Dijkstra
• Algorithme de Dantzig-Ford

• Portail de l’informatique
• Portail de la logique