Algorithme du lievre et de la tortue

L'algorithme de Floyd de détection de cycle, encore connu sous le nom d'algorithme du lièvre et de la tortue, est un algorithme pour détecter les cycles dans des séquences arbitraires, qu'il s'agisse de structures de données ou de séquences générées à la volée (et notamment les séquences pseudo-aléatoires), en espace O(1).

Cet algorithme fut énoncé par Robert Floyd en 1967^[1].

Il ne doit pas être confondu avec l'algorithme de Floyd-Warshall (tous les plus courts chemins dans un graphe).

Sommaire 1 Algorithme 1.1 Visualisation 1.2 Pseudo-code 2 Complexité 3 Variantes 4 Références 5 Liens externes

Algorithme

Soit

une fonction, et S un ensemble fini de cardinalité n. On considère la suite (a_i) définie par 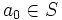et

a_{i + 1} = f(a_i)

Il est clair que cette suite aboutit nécessairement à un cycle, le nombre de ses valeurs possibles étant limité à n. Une manière naïve de déterminer la longueur de ce cycle consiste à stocker chaque élément de la séquence et, à chaque étape, de vérifier si le nouvel élément fait partie des éléments déjà rencontrés. L'espace utilisé est en O(μ + λ), où μ est la longueur du cycle et λ le nombre d'éléments à l'extérieur du cycle.

Si l'on parvient à trouver deux éléments de la séquence a_i et a_j tels que

a_i = a_j

alors | i − j | est un multiple de la longueur du cycle. L'algorithme de Floyd de détection de cycle détermine une telle égalité en parcourant la séquence simultanément à deux vitesses différentes, respectivement 1 et 2. L'algorithme aboutit nécessairement sur deux valeurs égales, i.e. détermine m tel que

a_m = a_2m

Dès lors, 2m − m = m est un multiple de la longueur du cycle, μ. Pour déterminer la valeur exacte de μ, il suffit de refaire tourner l'algorithme à partir de m+1, jusqu'à trouver un autre nombre m₁ tel que 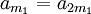. Dès lors on a d'une part 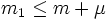(car on retombe alors sur a_m) et d'autre part μ qui divise m₁ − m (car il divise m et m₁), donc μ = m₁ − m.

Visualisation

La meilleure façon de visualiser l'algorithme consiste à représenter la séquence. Le dessin obtenu ressemble à la lettre grecque ρ. La séquence démarre en bas, monte et emprunte le cycle dans le sens des aiguilles d'une montre. Suivant l'algorithme de Floyd, les deux parcours se rencontrent en a₆ après 6 itérations. Un deuxième tour de l'algorithme amène les deux parcours à se rencontrer après 6 nouvelles itérations, d'où la valeur μ = 6.

Parcours	t0	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10	t11	t12
Lent	a0	a1	a2	a3	a4	a5	a6	a7	a2	a3	a4	a5	a6
Rapide	a0	a2	a4	a6	a2	a4	a6	a2	a4	a6	a2	a4	a6

Pseudo-code

 m := 1; x := f(a0); y := f(x);
 tant que x <> y faire
    m := m + 1;
    x := f(x);
    y := f(f(y));
 { la valeur de m est telle que am = a2m }

Si on souhaite obtenir la valeur de μ, il suffit d'ajouter à la suite le code suivant :

 mu := 0;
 répéter
    mu := mu+1;
    x := f(x);
    y := f(f(y));
 tant que x <> y

Complexité

L'algorithme effectue au minimum λ comparaisons, étant donné que le parcours lent de la séquence doit au moins atteindre le cycle pour rencontrer le parcours rapide. Le nombre maximum de comparaisons est λ + μ, étant donné que le parcours lent ne peut effectuer plus d'un tour du cycle avant d'être rattrapé par le parcours rapide. L'algorithme utilise un espace O(1).

Variantes

La variante la plus connue de l'algorithme de Floyd de détection de cycle est l'algorithme rho de Pollard, un algorithme de décomposition en produit de facteurs premiers qui utilise les séquences pseudo-aléatoires pour factoriser les entiers. Il existe également un algorithme de calcul du logarithme discret basé sur l'algorithme de Floyd de détection de cycle.

Références

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Floyd's cycle-finding algorithm ».

Liens externes

• Algorithme de Floyd de détection de cycle sur LiteratePrograms

• Portail de l’informatique