Hélimagnétisme

L'hélimagnétisme est une forme d'ordre magnétique, caractérisée par une très grande répétitivité spatiale, et qui résulte d'une compétition, à l'intérieur d'un même matériau, entre les interactions d'échanges ferromagnétique et antiferromagnétique. Il avait été prédit en 1959^[1] et découvert la même année dans le cas de l'alliage MnAu₂^[2].

C'est un état magnétique courant pour les terres rares, le plus souvent observé aux basses températures (celles de l'hélium liquide).

Au niveau macroscopique, l'aimantation totale d'un système hélimagnétique est nulle ou très faible, car les moments sont orientés dans toutes les directions du plan.

Description microscopique

L'hélimagnétisme se caractérise au niveau microscopique par une orientation des moments magnétiques voisins selon un motif en hélice. Il est possible de considérer l'antiferromagnétisme et le ferromagnétisme comme des cas d'hélimagnétisme limites, avec un pas d'hélice de 180° et 0°, respectivement.

L'hélimagnétisme pouvant présenter une rotation dans le sens horaire ou antihoraire, il casse la symétrie d'inversion spatiale des moments magnétiques.

Si le rapport entre le pas d'hélice et π est irrationnel, la structure est incommensurable.

Considérations énergétiques

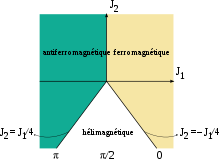Diagramme de phase de l'hélimagnétisme, du ferromagnétisme et de l'antiferromagnétisme. L'hélimagnétisme n'est favorisé que pour J₂ < 0, dans une zone où | J₁ | < 4 | J₂ | . Les structures ferromagnétique et antiferromagnétique peuvent être comprises comme un cas limite de l'hélimagnétisme pour un angle de pas d'hélice valant exactement 0 et ou exactement π, respectivement.

Dans les terres rares, l'interaction magnétique dominante est le couplage RKKY via les électrons de conduction. Cette interaction est connue pour changer de signe avec la distance. Si l'on considère un matériau cristallin présentant une telle interaction, on peut noter J0, J1 et J2 les constantes d'échange correspondant respectivement aux atomes d'un même plan cristallin, au premier et au second voisin.

On suppose que toutes les orientations des matériaux des moments magnétiques sont parallèles dans un plan donné et on appelle ϕ la différence d'angle d'aimantation entre le plan considéré et le plan des premiers voisins.

L'énergie du système est alors : E = − NS²(J₀ + 2J₁cos ϕ + 2J₂cos 2ϕ)

La minimisation de cette énergie conduit à l'équation : (J₁ + 4J₂cos ϕ)sin ϕ = 0

Cette équation admet les solutions suivantes :

• φ = 0, c'est-à-dire une orientation parallèle des moments : ferromagnétisme
• ϕ = π, orientation anti-parallèle des moments d'un plan sur l'autre : antiferromagnétisme
• , c'est l'hélimagnétisme.

L'hélimagnétisme n'est possible que si | J₁ | < 4 | J₂ | .

Si l'on introduit ces trois solutions dans l'expression de l'énergie, il vient :

• E(0) = 2NS²( − J₁ − J₂ − J₀ / 2)
• E(π) = 2NS²(J₁ + J₂ − J₀ / 2)
• (on utilise cos ϕ = − J₁ / (4J₂) et l'identité trigonométrique cos2ϕ = 2cos ²ϕ − 1)

Dans le cas J₂ > 0 et J₁ > 0, on calcule . Compte-tenu de | J₁ / (4J₂) | < 1 et des signes de J₁ et J₂, E(0) − E(ϕ) < 0. E(π) < E(0) est vérifié pour les mêmes raisons de signes. La configuration ferromagnétique est favorisée.

Dans le cas J₂ > 0 et J₁ < 0, on vérifie de même que est négatif. E(0) < E(π) est vérifié pour les mêmes raisons. La configuration antiferromagnétique est favorisée.

La configuration hélimagnétique, qui n'est possible que pour | J₁ | < 4 | J₂ | , n'est favorisée énergétiquement que pour J₂ < 0.

Notes et références

Bibliographie

• Étienne du Trémolet de Lacheisserie (coordinateur), Magnétisme I - Fondements, Presses universitaires de Grenoble, Grenoble, 2000 (ISBN 2868834639), p. 139-140.
• Stephen Blundell, Magnetism in Condensed Matter, Oxford University Press, Oxford, 2001 (ISBN 9780198505914), p. 99-100.

• Portail de la physique