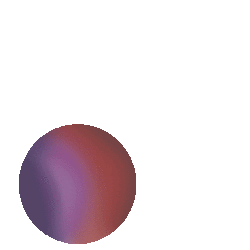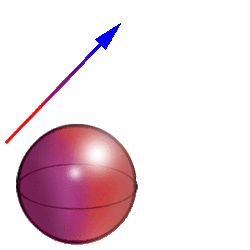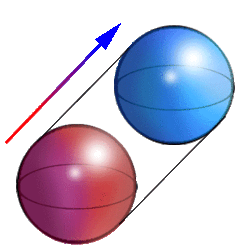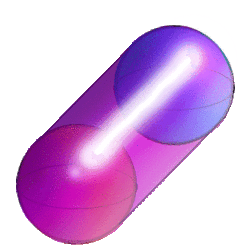- Cylindre sphérique
-
Construction d'un cylindre sphérique par translation d'une sphère de dimension 3 vers une quatrième dimension
En géométrie, un cylindre sphérique ou sphérindre est une forme géométrique généralisant le cylindre dans un espace à quatre dimensions. On peut l'obtenir en déplaçant une sphère (déjà centrée sur les axes x y et z) d'une unité le long de l'axe w : le cylindre sphérique est alors l'ensemble des positions prises par la sphère durant ce déplacement.
De la même façon qu'un cylindre de dimension 3 est fait de deux disques aux extrémités et d'un rectangle "tordu" délimité par leurs deux périmètres circulaires, le cylindre sphérique de dimension 4 est composé de deux sphères aux extrémités, et d'un cylindre de dimension 3 "tordu" délimité par leurs surfaces sphériques.
Si on intersecte le sphérindre avec un espace parallèle à l'espace xyz, on obtient une sphère ; si on intersecte le sphérindre avec un espace comprenant l'axe w, on obtient un cylindre droit unitaire ; sinon, lorsque l'espace de section est oblique, on obtient une ellipsoïde.
Sa caractéristique d'Euler-Poincaré vaut 0, comme celle d'une hypersphère de dimension 4.Notes et références
The spherical cylinder (sur Eusebeia) en anglais
Annexes
Articles connexes
Pour d'autres objets particuliers à 4 dimensions, voir aussi :
Wikimedia Foundation. 2010.
