Hidden Markov Models

Hidden Markov Models

Modèle de Markov caché

Page d'aide sur l'homonymie Pour les articles homonymes, voir MMC.

Un modèle de Markov caché (MMC) -- en anglais Hidden Markov Models (HMM) (ou plus correctement, mais moins employé automate de Markov à états cachés) est un modèle statistique dans lequel le système modélisé est supposé être un processus Markovien de paramètres inconnus.

Les modèles de Markov cachés sont massivement utilisés notamment en reconnaissance de formes, en intelligence artificielle ou encore en traitement automatique du langage naturel.

Sommaire

Modèle du sac en papier

Le jeu des sacs en papier

Imaginons un jeu simple, avec des sacs en papier (opaque) contenant des jetons numérotés.

À chaque tour du jeu nous tirons un jeton d'un sac et, en fonction du jeton, passons à un autre sac. Après chaque tour, le jeton est remis dans le sac, nous notons enfin la séquence des numéros tirés.

Exemple

Nous disposons de deux sacs, appelés A et B, ainsi que d'un ensemble de jetons numérotés a et b.

Dans chaque sac nous plaçons un certain nombre de jetons a et un certain nombre de jetons b : dans cet exemple, nous plaçons dans le sac A 19 jetons b et un seul jeton a. Dans le sac B nous plaçons 4 jetons a et un seul jeton b.

  • Nous commençons par piocher un jeton au hasard dans le sac A. Si l'on pioche un jeton a, on reste sur ce sac, si l'on pioche un jeton b, on passe au sac B. On note également quel jeton a été tiré et on le remet dans le sac.
  • On recommence cette étape avec le sac en cours, jusqu'à ce que le jeu s'arrête (au bon vouloir du joueur).

Nous avons les probabilités de passer à une station suivante :

Tirage suivant en A Tirage suivant en B
Station courante en A 0.05 0.95
Station courante en B 0.8 0.2

En jouant plusieurs parties, nous sommes susceptibles d'obtenir les séquences suivantes :

  • a b a b a b a a b a
  • a b b a b a b a b a
  • a b b a b b a b a b
  • ...

Ce jeu peut-être modélisé par une chaîne de Markov: chaque sac représente un état, la valeur du jeton donne la transition, la proportion de jeton d'une valeur est la probabilité de la transition.

Notre exemple du jeu du sac en papier est équivalent à l'automate de Markov suivant :

Exemple-markov-sac-papier.png

Le jeu des sacs en papier cachés

Nous reprenons en partie le modèle précédent mais introduisons de nouveaux types de sacs.

  • Des sacs pour savoir dans quel sac effectuer le prochain tirage ;
  • Des sacs de sortie pour générer la séquence ;

À partir de la séquence générée, il sera généralement impossible de déterminer quels tirages ont conduit à quelle séquence, la séquence de tirage dans les sacs donnant les transitions est inconnue, c'est pourquoi on parle de sacs en papier cachés.

Exemple

Repartons de l'exemple précédent. Nous conservons les sacs A et B, qui donnent les transitions, et ajoutons deux sacs A' et B' , situés juste à côté.

  • A' contient quatre jetons j et un jeton k ;
  • B' contient un jeton j et quatre jetons k.

Le jeu est le suivant :

  • On part du groupe de sac A, on tire un jeton dans le sac A', on consigne sa valeur et on le replace dans le sac ;
  • On tire un jeton dans le sac A pour savoir dans quel groupe de sac se feront les prochains tirages, on le replace ;
  • On recommence ces opérations autant de fois que le joueur le souhaite.

Le jeu génère deux séquences :

  • La séquence de sortie, connue, le résultat du jeu ;
  • La séquence des transitions, inconnue.

Pour cet exemple, nous avons pu générer les séquences suivantes :

Séquence de transition A B A B A B B A A A B A A B A B A B A B
Séquences de sortie j j k k j k k j k j j j j k k j k k j k

On observe que des séquences de transitions identiques peuvent donner des sorties différentes, et vice-versa.

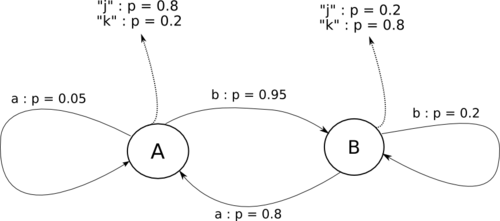
Ce jeu peut-être modélisé par un Automate de Markov à états cachés : les groupes de sacs sont les états, les tirages donnant le groupe de tirages suivant sont les transitions (avec la probabilité associée en fonction de la proportion des jetons dans le sac), les sacs de sortie donnent les valeurs de sortie de l'automate (même remarque pour la probabilité).

Le jeu précédent correspond donc à l'automate de Markov à états cachés suivant :

Exemple-markov-sac-papier-cache.png

Les flèches en pointillés indiquent les sorties probables à chaque passage dans un état.

Formalisme

Un automate de Markov à états cachés est un quadruplet {S,Π,A,B} des ensembles décrits suivant :

  • Si l'état i ;
  • πi la probabilité que Si soit l'état initial ;
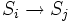  • aij la probabilité de la transition S_i \rightarrow S_j ;
  • bi(k) la probabilité d'émettre le symbole k étant dans l'état Si ;

sous contrainte :

  • ∑ πi = 1
    i
    la somme des probabilités des états initiaux est égale à 1 ;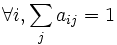
  • \forall i, \sum_{j} a_{ij} = 1 la somme des probabilités des transitions partant d'un état est égale à 1 ;
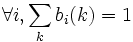  • \forall i, \sum_{k} b_{i}(k) = 1 la somme des probabilités des émissions partant d'un état est égale à 1.

Utilisation

Il y a trois exemples typiques de problème que l'on peut chercher à résoudre avec un HMM :

  • connaissant l'automate, calculer la probabilité d'une séquence particulière (se résout à l'aide de l'algorithme de Viterbi)
  • connaissant l'automate, trouver la séquence la plus probable d'état (caché) ayant conduit à la génération d'une séquence de sortie donnée (se résout également avec l'algorithme de Viterbi)
  • Étant donné une séquence de sortie, retrouver l'ensemble d'états le plus probable et les probabilités des sorties sur chaque état. Se résout avec l'algorithme de Baum-Welch, appelé aussi algorithme forward-backward.

Applications

Histoire

Les HMM ont été décrits pour la première fois dans une série de publication de statistiques par Leonard E. Baum et d'autres auteurs après 1965.

Ils ont été appliqués dès la fin des années 1970 à la reconnaissance vocale. Dans la seconde moitié des années 1980, les HMM ont commencé à être appliqués à l'analyse de séquences biologique, en particulier l'ADN.

Apprentissage des HMM

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Il existe plusieurs algorithmes pour réaliser l'apprentissage des HMM. On peut citer notamment :

Voir aussi

Ce document provient de « Mod%C3%A8le de Markov cach%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hidden Markov Models de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Hidden Markov model — Probabilistic parameters of a hidden Markov model (example) x mdash; states y mdash; possible observations a mdash; state transition probabilities b mdash; output probabilitiesA hidden Markov model (HMM) is a statistical model in which the system …   Wikipedia

  • Hidden Markov Model — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Es ist die einfachste Form eines dynamischen Bayes schen Netzes. Der erste Zufallsprozess entspricht dabei einer Markov Kette, die …   Deutsch Wikipedia

  • Hidden-Markov-Modell — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Hidden Markov Modell — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Hidden Markov model — Das Hidden Markov Model (HMM) ist ein stochastisches Modell, das sich durch zwei Zufallsprozesse beschreiben lässt. Ein Hidden Markov Model ist auch die einfachste Form eines dynamischen Bayesschen Netz. Der erste Zufallsprozess entspricht dabei… …   Deutsch Wikipedia

  • Hierarchical hidden Markov model — The Hierarchical hidden Markov model (HHMM) is a statistical model derived from the hidden Markov model (HMM). In an HHMM each state is considered to be a self contained probabilistic model. More precisely each stateof the HHMM is itself an HHMM …   Wikipedia

  • Layered hidden Markov model — The layered hidden Markov model (LHMM) is a statistical model derived from the hidden Markov model (HMM). A layered hidden Markov model (LHMM) consists of N levels of HMMs, where the HMMs on level i + 1 correspond to observation symbols or… …   Wikipedia

  • Markov chain — A simple two state Markov chain. A Markov chain, named for Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized …   Wikipedia

  • Markov model — In probability theory, a Markov model is a stochastic model that assumes the Markov property. Generally, this assumption enables reasoning and computation with the model that would otherwise be intractable. Contents 1 Introduction 2 Markov chain… …   Wikipedia

  • Hidden semi-Markov model — A hidden semi Markov model (HSMM) is a statistical model with the same structure as a hidden Markov model except that the unobservable process is semi Markov rather than Markov. This means that the probability of there being a change in the… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”