Géometrie métrique

Espace métrique

En mathématiques, un espace métrique est un ensemble au sein duquel une notion de distance entre les éléments de l'ensemble est définie. C'est un cas particulier d'espace topologique.

L'exemple correspondant le plus à notre expérience intuitive de l'espace est l'espace euclidien à trois dimensions. La métrique euclidienne de cet espace définit la distance entre deux points comme la longueur du segment les reliant.

Définitions

On appelle (E, d) un espace métrique si E est un ensemble non vide, et d une distance sur E.
On appelle distance sur un ensemble E, une application d de $E 2$ dans 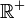$\mathbb{R}^+$ , telle que :

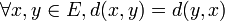$\forall x,y\in E, d(x,y)=d(y,x)$ (symétrie);
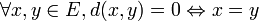$\forall x,y\in E, d(x,y)=0\Leftrightarrow x=y$ (séparation);
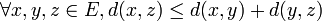$\forall x,y,z\in E, d(x,z)\leq d(x,y)+d(y,z)$ (inégalité triangulaire).

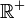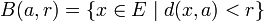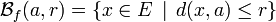On appelle boule ouverte (resp. fermée) centrée en un point a de E et de rayon r (un élément de $\mathbb{R}^+$ ), l'ensemble des points x situés à une distance de a strictement plus petite que r (resp. inférieure ou égale à r) : $B(a,r)=\{x\in E\mid d(x,a)<r \}$ , $\mathcal{B}_f(a,r)=\left\{x\in E\,\mid\,d(x,a)\leq r\right\}$ .

On appelle ouvert de E, tout ensemble U tel que pour tout x de U, il existe une boule ouverte de centre x, de rayon non nul, et incluse dans U: 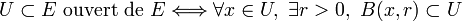$U \subset E\ \mathrm{ouvert\ de }\ E \Longleftrightarrow \forall x \in U,\ \exists r>0,\ B(x,r) \subset U$ . Un ouvert est une partie qui a une certaine « épaisseur » autour de ses points. La distance munit donc E d'une topologie dite « topologie induite par la distance » d. Un espace topologique est dit métrisable s'il existe une distance induisant sa topologie ; cette distance n'est jamais unique. Les notions de boule, de borné (c'est-à-dire inclus dans une boule), de suite de Cauchy, de continuité uniforme, etc. ne sont pas des notions topologiques mais métriques, susceptibles de varier selon la distance choisie. Dans cette topologie, les voisinages d'un point sont tous les sous-ensembles contenant une boule ouverte centrée sur ce point. La topologie usuelle sur la droite (des nombres réels), le plan, etc. sont des exemples de topologies définissables à l'aide d'une métrique.

Remarques

Une propriété intéressante des espaces topologiques métrisables est celle de séparation. En effet, si on choisit deux éléments distincts x et y d'un espace métrique E, leur distance notée δ est non nulle, par conséquent les boules ouvertes de centre x et y et de rayon δ/2 sont disjointes et sont des voisinages de x et y. Un espace métrique dispose d'une propriété du même ordre mais plus forte. Si A et B sont deux fermés disjoints il existe deux ouverts U contenant A et V contenant B qui sont disjoints. On dit qu'un espace métrique est normal (cf l'article Espace normal).

Une boule fermée de centre a et de rayon r est un fermé, pour la topologie induite. La notation 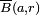$\scriptstyle{\overline{B}(a,r)}$ est également utilisée mais ambiguë, car B_f(a, r) est parfois différent de l'adhérence de B(a, r), au moins pour r = 0 (voir Adhérence (mathématiques) et Boule (mathématiques)).

Exemples

Une norme N induit de manière naturelle une distance d(x,y)=N(x-y).
La distance triviale (ou encore distance discrète ou métrique discrète) : sur un ensemble non vide, on décide que la distance entre deux points distincts est 1 (d(x,y) = 1 pour tout x différent de y et d(x,x) = 0). Avec une telle distance, on vérifie aisément que la topologie est alors l'ensemble des parties de $E$ , c'est-à-dire que toute partie F de E est ouverte.
Les espaces topologiques R et ]0,1[ sont homéomorphes, mais munis des distances usuelles, ils ne sont pas isomorphes en tant qu'espaces métriques ; par exemple R est complet mais ]0,1[ ne l'est pas.
Si on munit R₊ de la distance d(x,y)=|e^x- e^y|, on retrouve la topologie usuelle sur R₊ mais maintenant toutes les fonctions polynômes sont uniformément continues.
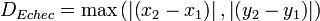
La distance aux échecs permet de connaître le nombre de coups nécessaire au jeu d'échec pour aller avec le roi d'une case x₁, y₁ à une case x₂, y₂ et se définit par $D_{Echec} = \max \left ( \left | \left ( x_2 - x_1 \right) \right | , \left | \left ( y_2 - y_1 \right ) \right | \right )$
La distance de Manhattan : dans le plan 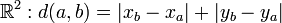$\mathbb R^2:d(a,b)=|x_b-x_a|+|y_b-y_a|$ .c'est bien sûr la distance induite par la norme 1.

Équivalence d'espaces métriques

En comparant deux espaces métriques il est possible de distinguer différents degrés d'équivalence. Pour préserver a minima la structure topologique induite par la métrique, une fonction continue entre les deux est requise.

Soit deux espaces métriques (M₁, d₁) et (M₂, d₂). M₁ et M₂ sont appelés

topologiquement isomorphes (ou homéomorphes) s'il existe un homéomorphisme entre eux.

uniformément isomorphes s'il existe un isomorphisme uniforme entre eux.

isométriquement isomorphes s'il existe un isométrie bijective entre eux. Dans ce cas les deux espaces sont essentiellement identiques. Une isométrie est une fonction f : M₁ → M₂ qui préserve les distances : d₂(f(x), f(y)) = d₁(x, y) pour tout x, y dans M₁. Les isométries sont forcément injectives.

similaire s'il existe une constante positive k > 0 et une fonction bijective f, appelée similarité telle que f : M₁ → M₂ et d₂(f(x), f(y)) = k d₁(x, y) pour tout x, y dans M₁.

similaire (du second type) s'il existe une fonction bijective f, appelée similarité telle que f : M₁ → M₂ et d₂(f(x), f(y)) = d₂(f(u), f(v)) si et seulement si d₁(x, y) = d₁(u, v) pour tout x, y,u, v dans M₁.

Dans le cas d'un espace euclidien avec la métrique usuelle, les deux notions de similarité sont équivalentes.

Voir aussi

Portail de la géométrie

Ce document provient de « Espace m%C3%A9trique ».

Catégories : Topologie | Espace métrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Géometrie métrique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Géométrie métrique — ● Géométrie métrique géométrie où l on étudie les propriétés des figures invariantes par les isométries … Encyclopédie Universelle
Géométrie métrique parabolique — ● Géométrie métrique parabolique géométrie non euclidienne … Encyclopédie Universelle
MÉTRIQUE — La métrique est l’étude des régularités systématiques qui caractérisent la poésie littéraire versifiée, qu’il s’agisse des formes de vers (mètre ), de groupes de vers (strophe ) ou de poèmes entiers (forme fixe ). Son domaine peut s’étendre à des … Encyclopédie Universelle
Geometrie — Géométrie La géométrie est la partie des mathématiques qui étudie les figures de l espace de dimension 3 (géométrie euclidienne) et, depuis le XVIIIe siècle, aux figures de d autres types d espaces (géométrie projective, géométrie non… … Wikipédia en Français
Géometrie — Géométrie La géométrie est la partie des mathématiques qui étudie les figures de l espace de dimension 3 (géométrie euclidienne) et, depuis le XVIIIe siècle, aux figures de d autres types d espaces (géométrie projective, géométrie non… … Wikipédia en Français
GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… … Encyclopédie Universelle
Géométrie — Traditionnellement, la géométrie est la partie des mathématiques qui étudie les figures du plan et de l espace (géométrie euclidienne). Depuis la fin du XVIIIe siècle, la géométrie étudie également les figures appartenant à d autres types d… … Wikipédia en Français
Geometrie de l'espace-temps dans les reperes tournants — Géométrie de l espace temps dans les repères tournants Nous allons aborder dans cet article la géométrie de l espace temps dans un repère en rotation. Plus spécifiquement nous considérerons un disque en rotation et nous allons voir quelle forme… … Wikipédia en Français
Géométrie De L'espace-Temps Dans Les Repères Tournants — Nous allons aborder dans cet article la géométrie de l espace temps dans un repère en rotation. Plus spécifiquement nous considérerons un disque en rotation et nous allons voir quelle forme prend la géométrie de l espace temps pour un observateur … Wikipédia en Français
Metrique riemannienne — Métrique riemannienne Les métriques riemanniennes sont les objets d étude de la géométrie riemannienne. La première introduction a été donnée par Riemann en 1854. Cependant, son article sur le sujet a été publié après sa mort, en 1868. La même… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Géometrie métrique

Espace métrique

Sommaire

Définitions

Exemples

Équivalence d'espaces métriques

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Géometrie métrique

Espace métrique

Sommaire

Définitions

Exemples

Équivalence d'espaces métriques

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link