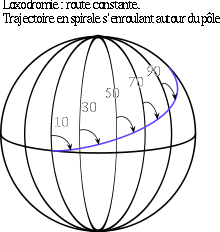
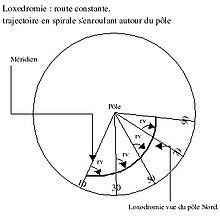
Loxodromie

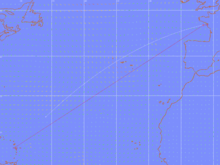Comparaison entre les trajectoires loxodromique (rouge) et orthodromique (blanc) sur une carte à projection de Mercator

Une loxodromie (du grec lox(o)- et -dromie course oblique), (en anglais rhumb line), est une courbe qui coupe les méridiens d'une sphère sous un angle constant.

Une route loxodromique est représentée sur une carte marine ou aéronautique en projection de Mercator par une ligne droite mais ne représente pas la distance la plus courte entre deux points. En effet, la route la plus courte, appelée route orthodromique ou orthodromie, est un grand cercle de la sphère.

La loxodromie est une trajectoire à route vraie constante. Elle doit son nom au géomètre portugais Pedro Nunes, qui le premier l'a distinguée d'un cercle (c 1537).{Stevin, Harriot l'ont étudiée ( c.1580) : c'est un des premiers cas d'«intégration difficile» connus}.

Navigation loxodromique

Le problème posé est celui de la détermination de la route et de la distance loxodromique entre deux points. Il s'agit donc du problème inverse de la navigation à l'estime.

• si les deux points A et B sont peu éloignés, on peut se contenter de formules approchées (latitude moyenne):

étant la distance parcourue à la route  ; et les coordonnées géographiques (latitude, longitude) des points A et B, et  :

et :

ces formules approchées restent précises à 1 mille marin près pour milles ( rappel : 1 mille = 1 minute d'arc ; soit 1 radian = 180*60/Pi = 3437.746770 minutes ; par ailleurs, il est convenu que la distance correspondant à 1 minute d'arc, s'appelle un mille marin et vaut : 40007,864km(soit le périmètre polaire de la Terre)/360/60 = 1.852 km.

• formules exactes (latitudes croissantes de la projection de Mercator) :

et :

est appelée la latitude croissante et vaut, en radians :

qui est la fonction de Gudermann inverse.

Démonstration mathématique

Sur le globe terrestre, les loxodromies correspondent (lorsqu'elles ne sont pas « dégénérées », c'est-à-dire lorsque l'angle initial donné n'est pas nul) à des spirales s'enroulant autour du pôle (le pôle Nord si l'angle initial et dans ]0,π[ et que le déplacement se fait dans le sens des latitudes croissantes).

Soit à déterminer une équation de la loxodromie et à calculer la longueur parcourue à cap constant .

Considérons les coordonnées sphériques habituelles sur la sphère unité : la longitude φ et la colatitude θ. La loxodromie constitue un arc sur la sphère que l'on suppose de classe C¹ :  ; soit la fonction qui à la longitude φ associe le point courant de la loxodromie de longitude φ et de colatitude θ(φ). Il faut donc bien sûr se donner au départ une origine des longitudes, puisqu'à un φ donné à 2π près, correspond une infinité de points distincts sur l'arc, de colatitudes différentes. Partons de l'équateur et suivons la loxodromie vers le pôle Nord en nous refusant les classes modulo 2π pour φ : par exemple .

Un vecteur tangent à la loxodromie est ainsi . Ce vecteur, qui dirige la tangente à l'arc, forme donc, par hypothèse, un angle α avec tout vecteur (non nul) dirigeant le parallèle au point considéré. Un vecteur dirigeant le parallèle en M(φ,θ(φ)) est (tandis qu'un vecteur dirigeant le méridien est ).

Dans la suite, pour alléger l'écriture, on ne précisera plus le point (φ,θ(φ)) auquel sont prises les fonctions et leurs dérivées partielles.

En effectuant le produit scalaire d'un vecteur directeur de la tangente à la loxodromie et d'un vecteur directeur du parallèle, on obtient le produit des normes de ces vecteurs par le cosinus de l'angle qu'ils forment :

, en notant le produit scalaire par .

En élevant au carré :

.

On a d'autre part : (les parallèles et les méridiens sont orthogonaux). Donc, par application du théorème de Pythagore, l'expression se réduit à :

.

Et en simplifiant :

.

D'où, avec « 1 − sin ² = cos ² »

.

Calculons les deux normes intervenant dans cette équation :

on sait, d'après le paramétrage sphérique rapporté aux coordonnées cartésiennes dans la base , que , où est le vecteur unitaire radial du plan équatorial défini par : . On définit comme le vecteur dérivé par rapport à φ de  : . Alors et . Ainsi, et .

L'équation se réduit à :

et puisque l'on a supposé un trajet vers le pôle Nord, θ est une fonction décroissante de φ et θ' < 0, on suppose là de plus (dans les autres cas, on déduit l'arc par une symétrie centrale et/ou une rotation convenable(s), donc on ne perd pas de généralité), par suite :

sin αsin θ(φ) = − θ'(φ)cos α

et , équation différentielle non linéaire à variables séparables en θ(φ)

En séparant les variables et en intégrant entre 0 et φ :

,

soit : (cf. Table de primitives)

La longueur L parcourue vaut alors, par définition :

où et et pour les mêmes raisons de signe, .

En changeant de variable, avec avec θ étant la colatitude, celle-çi variant de à 0 quand φ varie de 0 à  :

On a

Il est facile de vérifier le résultat, en prenant α égal à , on voit que l'arc parcouru est le méridien et sa longueur est égale au quart de la circonférence.

Voir aussi

Articles connexes

• orthodromie
• navigation à l'estime
• route (navigation)

Liens externes

• (fr) "Quelques Problèmes Mathématiques liés à la Navigation"
• (fr) "Logiciel de calcul de distances (loxodromiques et orthodromiques) et de caps"

• Portail du monde maritime
• Portail de l’aéronautique
• Portail de la géométrie