- Genre espace
-
Genre (relativité)
En relativité restreinte et en relativité générale, le genre d'un quadrivecteur est déterminé par le signe de sa norme. Selon celui-ci, on parle de genre temps, genre espace, ou genre lumière. Par extension, on parle de trajectoire de genre temps, de genre espace, ou de genre lumière quand le vecteur tangent à celle-ci est toujours du genre considéré.
Sommaire
Définition
Le genre d'un quadrivecteur V est déterminé par sa norme, c'est-à-dire par la quantité
- N = gabVaVb,
où g correspond à la métrique de l'espace considéré (la métrique de Minkowski en relativité restreinte, et la métrique associée à la variété différentielle décrivant l'espace temps en relativité générale).
Genre lumière
Quand la quantité N est nulle, le vecteur est dit de genre lumière. C'est ce qu'il se produit quand le vecteur correspond au vecteur tangent à la trajectoire d'un photon.
Genre espace et genre temps
La définition de genre espace et de genre temps dépend de la convention utilisée pour décrire la signature de la métrique. Pour les auteurs pour lesquels la signature de la métrique est (-+++), alors les vecteurs de genre temps sont tels que N est négatif et les vecteurs de genre espace ont tels que N est positif, alors que si l'on se place dans la convention où la signature de la métrique est (+---), les vecteurs de genre temps sont tels que N est positif et ceux de genre espace sont tels que N est négatif.
Indépendamment de la convention choisie, un vecteur de genre temps correspond à une trajectoire susceptible d'être empruntée par un objet physique. Un vecteur de genre espace ne correspond ni à une trajectoire possible d'un objet, ni à celle d'une trajectoire d'une particule sans masse.
Exemples
Dans la métrique de Minkowski, on peut définir les vecteur de base associés à un système de coordonnées cartésiennes (t,x,y,z). Ces vecteurs, que l'on peut noter
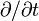 ou t, et ainsi de suite, et de composantes ta = (1,0,0,0) et ainsi de suite, possèdent les normes suivantes (dans la convention de signature (+---)) :
ou t, et ainsi de suite, et de composantes ta = (1,0,0,0) et ainsi de suite, possèdent les normes suivantes (dans la convention de signature (+---)) :- ηabtatb = c2 (c est la vitesse de la lumière)
- ηabxaxb = − 1,
- ηabyayb = − 1,
- ηabzazb = − 1.
Les vecteurs x, y, z sont ainsi de genre espace, alors que t est de genre temps. t correspond de fait à la quadrivitesse d'un observateur immobile dans le système de coordonnées considéré. À l'inverse, x, y, ou z ne correspond pas à la quadrivitesse d'un objet matériel, mais à une direction orthogonale à celle-ci. Ils décrivent une direction d'espace. Un vecteur du type
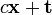 est lui de norme nulle :
est lui de norme nulle :- ηab(cxa + ta)(cxb + tb) = 0.
- Portail de la physique
Catégories : Relativité | Relativité générale
Wikimedia Foundation. 2010.
