GEONExT

GEONExT
GEONExT
Importez le logo de ce logiciel
Geonext-Carre2.gif
Manipulation des objets géométriques euclidiens dans le plan
Développeur Université de Bayreuth
Dernière version 1.73 (20 octobre. 2008) [+/−]
Environnement avec Java 1.4.*
Type Géométrie dynamique
Licence GPL
Site web http://geonext.uni-bayreuth.de/
modifier Consultez la documentation du modèle

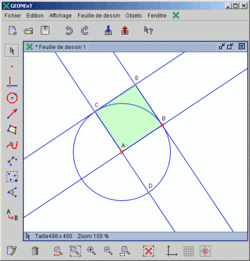
GEONExT est un logiciel de géométrie dynamique en 2D, c'est-à-dire qu'il permet de manipuler des objets géométriques du plan (cercle, droite et angle, par exemple) et de voir immédiatement le résultat. Il est principalement utilisé par des enseignants. Il vient aussi avec un ensemble de fonctions algébriques.

La graphie Geonext est techniquement une faute, mais est tolérée en pratique.

Sommaire

Description

Il permet d'explorer la géométrie euclidienne. Des chercheurs en géométrie peuvent l'utiliser pour valider de nouvelles constructions ou des constructions difficilement réalisables sur papier, telle les huit cercles d’Apollonius.

Lorsque comparé au tracé sur feuille de papier, son intérêt tient à ce qu'il est possible d'établir des liens entre les différents objets (par exemple, parallélisme et bissectrice d'un angle) et le logiciel maintient ceux-ci par après.

Il est principalement utilisé par des enseignants, mais toute personne souhaitant explorer de façon visuelle les transformations euclidiennes dans le plan en tirera profit.

Entièrement développé en Java, ce logiciel est en théorie fonctionnel pour tout système d'exploitation : Windows, Linux, Mac OS, etc. Il suffit de le lancer via une page HTML qui vient avec la distribution.

Une fois le logiciel lancé, l'utilisateur peut manipuler les différents objets géométriques de base dans un plan : cercle, droite, angle, etc.

Ce logiciel peut aussi s'exécuter depuis un poste d'ordinateur non connecté à Internet.

Venant avec une licence GNU, n'importe qui peut l'utiliser, l'étudier et le modifier. Dans tous les cas, certaines restrictions s'appliquent, mais aucune qui empêche de l'utiliser et de le répliquer autant que souhaité.

Afin d'utiliser correctement GEONExT, l'environnement d'exécution Java (JRE) doit être installé.

Histoire

Il a été développé à l'Université de Bayreuth (à Bayreuth, en Allemagne), qui le maintient toujours.

Voir aussi

Articles connexes

Liens externes

Géométrie dynamique
Logiciels
C.a.R. - Cabri Géomètre - GeoGebra - CaRMetal - DrGeo - Kig - GéoPlan - GéoSpace - GEONExT - TracenPoche
Cette boîte : v · Portail de la géométrie
  • Portail des logiciels libres Portail des logiciels libres

    • Wikimedia Foundation. 2010.

    Contenu soumis à la licence CC-BY-SA. Source : Article GEONExT de Wikipédia en français (auteurs)

    Regardez d'autres dictionnaires:

    • Geonext — Manipulation des objets géométriques euclidiens dans le plan …   Wikipédia en Français

    • GEONExT — Basisdaten Aktuelle Version: 1.73 (21. Oktober 2008) Betriebssystem: GNU/Linux …   Deutsch Wikipedia

    • Geonext — Basisdaten Aktuelle Version 1.73 (21. Oktober 2008) Betriebssystem …   Deutsch Wikipedia

    • List of interactive geometry software — Interactive geometry software (IGS, or dynamic geometry environments, DGEs) are computer programs which allow one to create and then manipulate geometric constructions, primarily in plane geometry. In most IGS, one starts construction by putting… …   Wikipedia

    • Список систем интерактивной геометрии — Содержание 1 Сравнение интерактивных геометрических систем 1.1 Лицензиро …   Википедия

    • Direktrix — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… …   Deutsch Wikipedia

    • Ellipse (Geometrie) — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… …   Deutsch Wikipedia

    • Ellipsenzirkel — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… …   Deutsch Wikipedia

    • Hauptscheitel — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… …   Deutsch Wikipedia

    • Nebenscheitel — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… …   Deutsch Wikipedia

    Share the article and excerpts

    Direct link
    … Do a right-click on the link above
    and select “Copy Link”