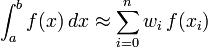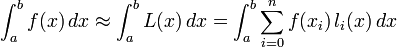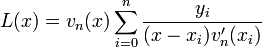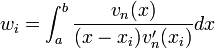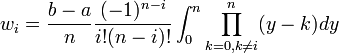Formules de newton-cotes

Formules de Newton-Cotes

En analyse numérique, les formules de Newton-Cotes, du nom d'Isaac Newton et de Roger Cotes, sont un ensemble de formules pour le calcul numérique d'une intégrale.

La fonction f est connu à des points équidistants $x i$ , pour i = 0, ..., n. Les formules de degré n sont définies ainsi :

$\int_a^b f(x) \,dx \approx \sum_{i=0}^n w_i\, f(x_i)$

où $x i = i h + x 0$ , les $w i$ sont appelés les coefficients de quadrature. Comme vous pouvez le voir dans l'écriture qui suit, ces poids dérivent d'une base lagrangienne de polynômes. Ils ne dépendent que des x_i et absolument pas de la fonction f. L(x) est l'interpolation lagrangienne pour les points ((x₀, f(x₀) ) ,.., (x_n, f(x_n) ).

$\int_a^b f(x) \,dx \approx \int_a^b L(x)\,dx = \int_a^b \sum_{i=0}^n f(x_i)\, l_i(x)\, dx$

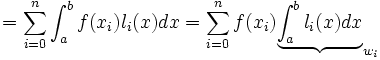
$=\sum_{i=0}^n \int_a^b f(x_i) l_i(x) dx=\sum_{i=0}^n f(x_i) \underbrace{ \int_a^b l_i(x) dx}_{w_i}$

Une formule de Newton-Cotes peut être établie à n'importe quel degré. Toutefois, la non-stabilité et la non-convergence des formules de Newton-Cotes contraint à n'utiliser que les degrés 1 ou 2.

Degré	Nom commun	Formule	Terme d'erreur
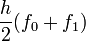
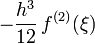
1	Méthode des trapèzes	$\frac{h}{2} (f_0 + f_1)$	$-\frac{h^3}{12}\,f^{(2)}(\xi)$
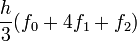
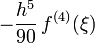
2	Méthode de Simpson 1/3	$\frac{h}{3} (f_0 + 4 f_1 + f_2)$	$-\frac{h^5}{90}\,f^{(4)}(\xi)$
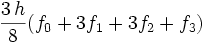
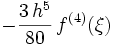
3	Méthode de Simpson 3/8	$\frac{3\, h}{8} (f_0 + 3 f_1 + 3 f_2 + f_3)$	$-\frac{3\, h^5}{80}\,f^{(4)}(\xi)$
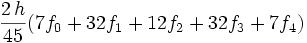
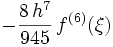
4	Méthode de Boole ur Méthode de Bode	$\frac{2\, h}{45} (7 f_0 + 32 f_1 + 12 f_2 + 32 f_3 + 7 f_4)$	$-\frac{8\, h^7}{945}\,f^{(6)}(\xi)$

Démonstration

Le polynôme d'interpolation $L (x)$ de f est (Voir Interpolation lagrangienne) :

$L(x)=v_n(x) \sum_{i=0}^n \frac{y_i}{(x-x_i)v'_n(x_i)}$

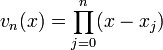où $v_n(x)=\prod^{n}_{j=0}(x-x_j)$ . D'où

$w_i=\int_a^b \frac{v_n(x)}{(x-x_i)v'_n(x_i)}dx$

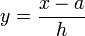
On effectue le changement de variable $y=\frac{x-a}{h}$

$w_i= \frac{b-a}{n}\frac{(-1)^{n-i}}{i!(n-i)!} \int_0^n \prod_{k=0,k \ne i}^n (y - k)dy$

Application pour n = 1

$\begin{matrix} w_0 &=& h \frac{(-1)^{1-0}}{0!(1-0)!} \int_0^1 \prod_{k=0,k \ne 0}^1 (y - k)dy \\ &=& -h \int_0^1(y-1)dy \\ &=& -h \left[ \frac{(y-1)^2}{2} \right]^1_0 \\ &=& \frac{h}{2} \end{matrix}$
Idem pour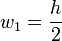 $w_1 = \frac{h}{2}$

Liens externes

Formules de Newton-Cotes sur Math-Linux.com

Ce document provient de « Formules de Newton-Cotes ».

Catégories : Intégration numérique | Isaac Newton

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formules de newton-cotes de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Formules De Newton-Cotes — En analyse numérique, les formules de Newton Cotes, du nom d Isaac Newton et de Roger Cotes, sont un ensemble de formules pour le calcul numérique d une intégrale. La fonction f est connu à des points équidistants xi, pour i = 0, ..., n. Les… … Wikipédia en Français
Formules de Newton-Cotes — En analyse numérique, les formules de Newton Cotes, du nom d Isaac Newton et de Roger Cotes, sont un ensemble de formules pour le calcul numérique d une intégrale. La fonction f est connu à des points équidistants xi, pour i = 0, ..., n. Les… … Wikipédia en Français
Formule de Newton-Cotes — En analyse numérique, les formules de Newton Cotes, du nom d Isaac Newton et de Roger Cotes, servent au calcul numérique d une intégrale sur un intervalle réel , ceci à l’aide d’une interpolation polynomiale de la fonction en des points répartis… … Wikipédia en Français
Liste Des Équations Et Formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X … Wikipédia en Français
Liste des equations et formules — Liste des équations et formules Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H … Wikipédia en Français
Liste des équations et formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X … Wikipédia en Français
Liste d'équations et formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X … Wikipédia en Français
Roger Cotes — Naissance 10 août 1682 Burbage (Angleterre) Décès 5 juin 1716 Cambridge (Angleterre) Domicile Royaume Uni Nationalité … Wikipédia en Français
Formules trigonométriques — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
Trigonométrie classique et formules — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formules de newton-cotes