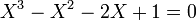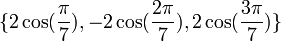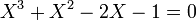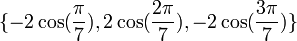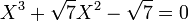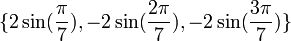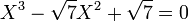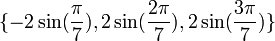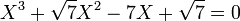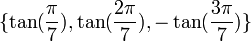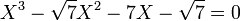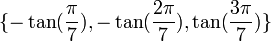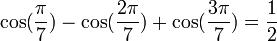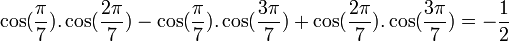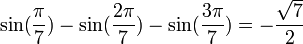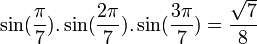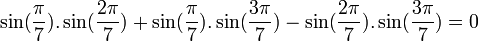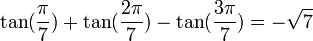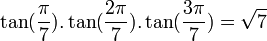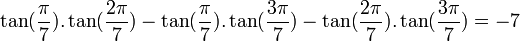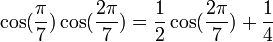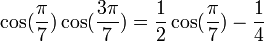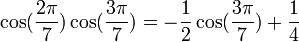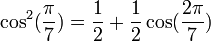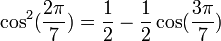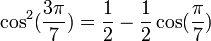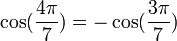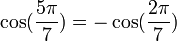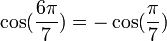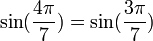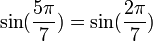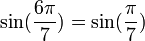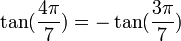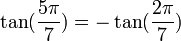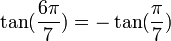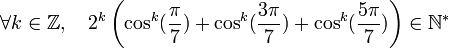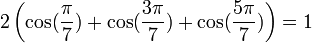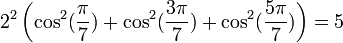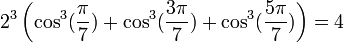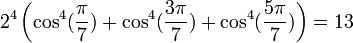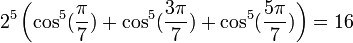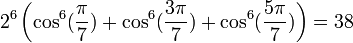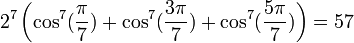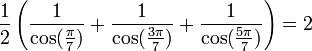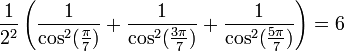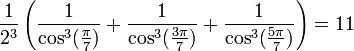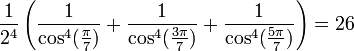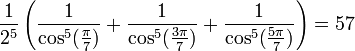Formules Trigonométriques En Kπ/7

Formules Trigonométriques En Kπ/7: Formules trigonométriques en kπ/7

Cet article répertorie les formules trigonométriques en kπ/7.

Sommaire

1 valeur approchée

2 Quelques solutions d'équations

3 Formules homogènes

4 Formules de linéarisation

5 Formules déductives

6 Propriétés remarquables

valeur approchée

Nous avons avec une assez bonne approximation:

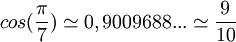
$cos(\frac{\pi}{7}) \simeq 0,9009688... \simeq \frac{9}{10} ~$

Cette valeur peut nous permettre de construire à la régle et au compas un angle ayant une mesure proche de 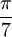$\frac{\pi}{7}$ .

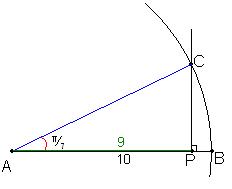
On trace un segment [AB] et un point P tel que :

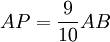
$AP = \frac{9}{10}AB ~$

Soit C le point d'interception entre le cercle de centre A et de rayon AB avec la perpendiculaire à (AB) passant par P.

Alors l'angle :

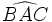
$\widehat{BAC} ~$

a approximativement une mesure de 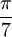$\frac{\pi}{7}$ .

Quelques solutions d'équations

L'équation :

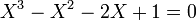
$X^3 - X^2 -2X +1 = 0 ~$

a pour racines :

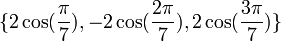
$\{2\cos(\frac{\pi}{7}), -2\cos(\frac{2\pi}{7}), 2\cos(\frac{3\pi}{7})\} ~$

L'équation :

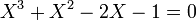
$X^3 + X^2 -2X - 1 = 0 ~$

a pour racines :

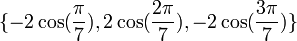
$\{-2\cos(\frac{\pi}{7}),2\cos(\frac{2\pi}{7}),-2\cos(\frac{3\pi}{7})\} ~$

L'équation :

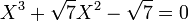
$X^3 + \sqrt{7}X^2 - \sqrt{7} = 0 ~$

a pour racines :

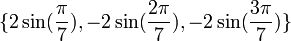
$\{2\sin(\frac{\pi}{7}),-2\sin(\frac{2\pi}{7}),-2\sin(\frac{3\pi}{7})\} ~$

L'équation :

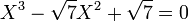
$X^3 - \sqrt{7}X^2 + \sqrt{7} = 0 ~$

a pour racines :

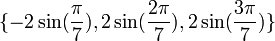
$\{-2\sin(\frac{\pi}{7}),2\sin(\frac{2\pi}{7}),2\sin(\frac{3\pi}{7})\} ~$

L'équation :

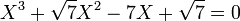
$X^3 + \sqrt{7}X^2 - 7X + \sqrt{7} = 0 ~$

a pour racines :

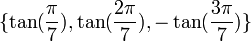
$\{\tan(\frac{\pi}{7}),\tan(\frac{2\pi}{7}),-\tan(\frac{3\pi}{7})\} ~$

L'équation :

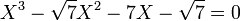
$X^3 - \sqrt{7}X^2 - 7X - \sqrt{7} = 0 ~$

a pour racines :

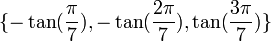
$\{-\tan(\frac{\pi}{7}),-\tan(\frac{2\pi}{7}),\tan(\frac{3\pi}{7})\} ~$

Formules homogènes

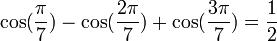
$\cos(\frac{\pi}{7}) - \cos(\frac{2\pi}{7}) + \cos(\frac{3\pi}{7}) = \frac{1}{2}~$

$\cos(\frac{\pi}{7}) . \cos(\frac{2\pi}{7}) . \cos(\frac{3\pi}{7}) = -\frac{1}{8}~$

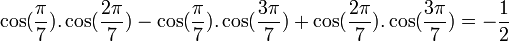
$\cos(\frac{\pi}{7}).\cos(\frac{2\pi}{7}) - \cos(\frac{\pi}{7}).\cos(\frac{3\pi}{7}) + \cos(\frac{2\pi}{7}).\cos(\frac{3\pi}{7}) = -\frac{1}{2}~$

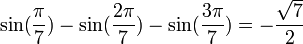
$\sin(\frac{\pi}{7}) - \sin(\frac{2\pi}{7}) - \sin(\frac{3\pi}{7}) = -\frac{\sqrt{7}}{2}~$

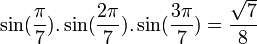
$\sin(\frac{\pi}{7}) . \sin(\frac{2\pi}{7}) . \sin(\frac{3\pi}{7}) = \frac{\sqrt{7}}{8}~$

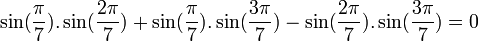
$\sin(\frac{\pi}{7}).\sin(\frac{2\pi}{7}) + \sin(\frac{\pi}{7}).\sin(\frac{3\pi}{7}) - \sin(\frac{2\pi}{7}).\sin(\frac{3\pi}{7}) = 0 ~$

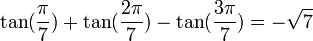
$\tan(\frac{\pi}{7}) + \tan(\frac{2\pi}{7}) - \tan(\frac{3\pi}{7}) = -\sqrt{7}~$

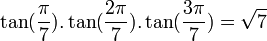
$\tan(\frac{\pi}{7}) . \tan(\frac{2\pi}{7}) . \tan(\frac{3\pi}{7}) = \sqrt{7}~$

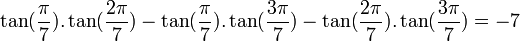
$\tan(\frac{\pi}{7}).\tan(\frac{2\pi}{7}) - \tan(\frac{\pi}{7}).\tan(\frac{3\pi}{7}) - \tan(\frac{2\pi}{7}).\tan(\frac{3\pi}{7}) = -7~$

Formules de linéarisation

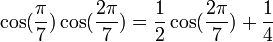
$\cos(\frac{\pi}{7})\cos(\frac{2\pi}{7}) = \frac{1}{2}\cos(\frac{2\pi}{7}) + \frac{1}{4} ~$

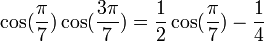
$\cos(\frac{\pi}{7})\cos(\frac{3\pi}{7}) = \frac{1}{2}\cos(\frac{\pi}{7}) - \frac{1}{4} ~$

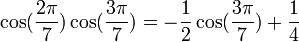
$\cos(\frac{2\pi}{7})\cos(\frac{3\pi}{7}) = -\frac{1}{2}\cos(\frac{3\pi}{7}) + \frac{1}{4} ~$

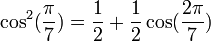
$\cos^2(\frac{\pi}{7}) =\frac{1}{2} + \frac{1}{2}\cos(\frac{2\pi}{7}) ~$

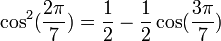
$\cos^2(\frac{2\pi}{7}) =\frac{1}{2} - \frac{1}{2}\cos(\frac{3\pi}{7}) ~$

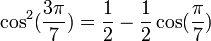
$\cos^2(\frac{3\pi}{7}) =\frac{1}{2} - \frac{1}{2}\cos(\frac{\pi}{7}) ~$

Formules déductives

Pour d'autres valeurs de k dans kπ/7, on peut se ramener aux formules précédentes en tenant compte du fait que :

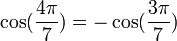
$\cos(\frac{4\pi}{7}) = -\cos(\frac{3\pi}{7}) ~$

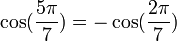
$\cos(\frac{5\pi}{7}) = -\cos(\frac{2\pi}{7}) ~$

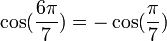
$\cos(\frac{6\pi}{7}) = -\cos(\frac{\pi}{7}) ~$

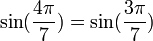
$\sin(\frac{4\pi}{7}) = \sin(\frac{3\pi}{7}) ~$

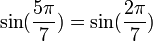
$\sin(\frac{5\pi}{7}) = \sin(\frac{2\pi}{7}) ~$

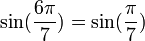
$\sin(\frac{6\pi}{7}) = \sin(\frac{\pi}{7}) ~$

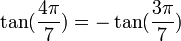
$\tan(\frac{4\pi}{7}) = -\tan(\frac{3\pi}{7}) ~$

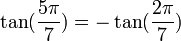
$\tan(\frac{5\pi}{7}) = -\tan(\frac{2\pi}{7}) ~$

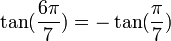
$\tan(\frac{6\pi}{7}) = -\tan(\frac{\pi}{7}) ~$

Propriétés remarquables

Nous avons :

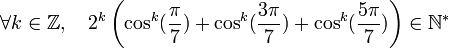
$\forall k \in \mathbb{Z}, \quad2^k\left(\cos^k(\frac{\pi}{7}) + \cos^k(\frac{3\pi}{7}) + \cos^k(\frac{5\pi}{7}) \right) \in \mathbb{N}^* ~$

Pour les premières valeurs de k positive, on obtient :

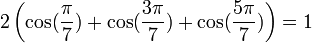
$2\left(\cos(\frac{\pi}{7}) + \cos(\frac{3\pi}{7}) + \cos(\frac{5\pi}{7})\right) = 1 ~$

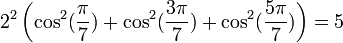
$2^2\left(\cos^2(\frac{\pi}{7}) + \cos^2(\frac{3\pi}{7}) + \cos^2(\frac{5\pi}{7})\right) = 5 ~$

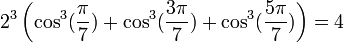
$2^3\left(\cos^3(\frac{\pi}{7}) + \cos^3(\frac{3\pi}{7}) + \cos^3(\frac{5\pi}{7})\right) = 4 ~$

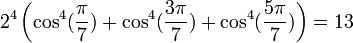
$2^4\left(\cos^4(\frac{\pi}{7}) + \cos^4(\frac{3\pi}{7}) + \cos^4(\frac{5\pi}{7})\right) = 13 ~$

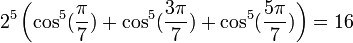
$2^5\left(\cos^5(\frac{\pi}{7}) + \cos^5(\frac{3\pi}{7}) + \cos^5(\frac{5\pi}{7})\right) = 16 ~$

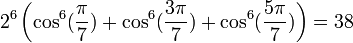
$2^6\left(\cos^6(\frac{\pi}{7}) + \cos^6(\frac{3\pi}{7}) + \cos^6(\frac{5\pi}{7})\right) = 38 ~$

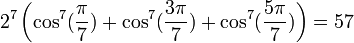
$2^7\left(\cos^7(\frac{\pi}{7}) + \cos^7(\frac{3\pi}{7}) + \cos^7(\frac{5\pi}{7})\right) = 57 ~$

etc.

Pour les premières valeurs de k négative, on obtient :

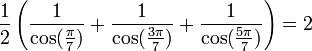
$\frac{1}{2}\left(\frac{1}{\cos(\frac{\pi}{7})} + \frac{1}{\cos(\frac{3\pi}{7})} + \frac{1}{\cos(\frac{5\pi}{7})}\right) = 2 ~$

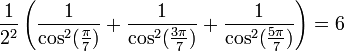
$\frac{1}{2^2}\left(\frac{1}{\cos^2(\frac{\pi}{7})} + \frac{1}{\cos^2(\frac{3\pi}{7})} + \frac{1}{\cos^2(\frac{5\pi}{7})}\right) = 6 ~$

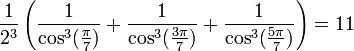
$\frac{1}{2^3}\left(\frac{1}{\cos^3(\frac{\pi}{7})} + \frac{1}{\cos^3(\frac{3\pi}{7})} + \frac{1}{\cos^3(\frac{5\pi}{7})}\right) = 11 ~$

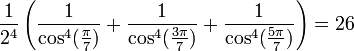
$\frac{1}{2^4}\left(\frac{1}{\cos^4(\frac{\pi}{7})} + \frac{1}{\cos^4(\frac{3\pi}{7})} + \frac{1}{\cos^4(\frac{5\pi}{7})}\right) = 26 ~$

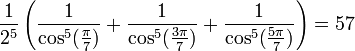
$\frac{1}{2^5}\left(\frac{1}{\cos^5(\frac{\pi}{7})} + \frac{1}{\cos^5(\frac{3\pi}{7})} + \frac{1}{\cos^5(\frac{5\pi}{7})}\right) = 57 ~$

etc.

Portail des mathématiques

Ce document provient de « Formules trigonom%C3%A9triques en k%CF%80/7 ».

Catégorie : Trigonométrie

Contenu soumis à la licence CC-BY-SA. Source : Article Formules Trigonométriques En Kπ/7 de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Formules trigonometriques en kπ/7 — Formules trigonométriques en kπ/7 Cet article répertorie les formules trigonométriques en kπ/7. Sommaire 1 valeur approchée 2 Quelques solutions d équations 3 Formules homogènes 4 … Wikipédia en Français
Formules trigonométriques en kπ/7 — Cet article répertorie les formules trigonométriques en kπ/7. Sommaire 1 valeur approchée 2 Quelques solutions d équations 3 Formules homogènes 4 … Wikipédia en Français
Formules trigonométriques — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
Formules de Simpson — Trigonométrie Planche sur la Trigonométrie, 1728 Cyclopaedia La trigonométrie (du grec ancien τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations… … Wikipédia en Français
Formules d'Euler — Formule d Euler Formule d Euler … Wikipédia en Français
Identités trigonométriques — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
Trigonométrie classique et formules — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
SÉRIES TRIGONOMÉTRIQUES — Les séries trigonométriques se sont introduites au XVIIIe et au début du XIXe siècle, en liaison avec certains problèmes de physique (mouvement des cordes vibrantes, propagation de la chaleur). Elles sont d’un usage courant en astronomie, en… … Encyclopédie Universelle
Histoire des fonctions trigonométriques — Tablette Plimpton 322 L’histoire des fonctions trigonométriques semble avoir débuté il y a environ 4 000 ans. Nous savons de façon certaine que les Babyloniens déterminaient des approximations de mesures d angles ou de longueurs de côtés de… … Wikipédia en Français
Histoire Des Fonctions Trigonométriques — Tablette Plimpton 322 L histoire des fonctions trigonométriques semble avoir débuté il y a environ 4 000 ans. Nous savons de façon certaine que les Babyloniens déterminaient des approximations de mesures d angles ou de longueurs de côtés de… … Wikipédia en Français

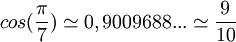
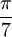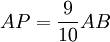
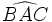
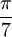Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts