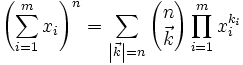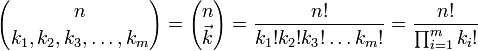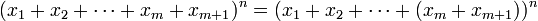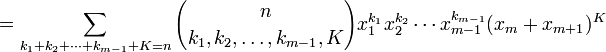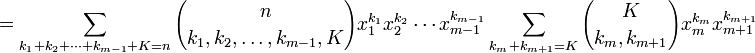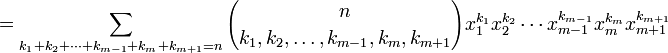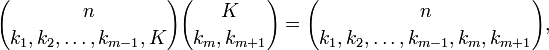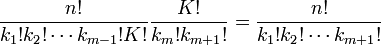- Formule Du Multinôme De Newton
-
Formule du multinôme de Newton
En mathématiques, la formule du multinôme de Newton est une relation donnant le développement d'une puissance entière n d'une somme d'un nombre fini m de termes sous forme d'une somme de produits de puissances de ces termes affectés de coefficients. Nous avons pour tous entiers naturels m et n, et pour tous réels ou complexes
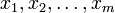 ,
,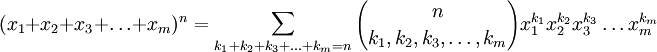 .
.
La somme porte sur toutes les combinaisons d'indices entiers naturels
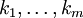 tels que
tels que 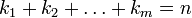 , certains d'entre eux pouvant être nuls.
, certains d'entre eux pouvant être nuls.Une écriture équivalente mais bien plus concise consiste à sommer sur tous les multi-indices
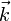 de dimension m dont le module
de dimension m dont le module 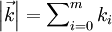 est égal à n :
est égal à n :Les nombres
sont appelés les coefficients multinomiaux.
La formule du binôme s'obtient comme cas particulier de la formule du multinôme, pour m = 2 ; et dans ce cas les coefficients multinomiaux sont les coefficients binomiaux.
Démonstration
Cette preuve utilise la formule du binôme. On fait une preuve par récurrence sur m.
(i) Pour m = 1, les deux côtés valent
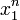 .
.(ii) Supposons le théorème vrai au rang m. Alors
par hypothèse de récurrence. Puis en appliquant le binome de Newton au dernier facteur, il vient que,
ce qui termine la récurrence. Pour la dernière étape, on a utilisé le fait que
car
Exemples
Voyez également
- Portail des mathématiques
Catégorie : Analyse combinatoire
Wikimedia Foundation. 2010.