Formule de Weizsäcker

La formule de Weizsäcker, appelée aussi formule de Bethe-Weizsäcker, est une formule semi-empirique donnant une valeur approximative de l'énergie de liaison nucléaire B caractérisant la liaison entre les nucléons qui constituent le noyau des atomes (voir un résumé dans Modèle de la goutte liquide). Son nom provient des inventeurs de la formule, à savoir Carl Friedrich von Weizsäcker et Hans Bethe.

Sommaire

1 Expression
2 Explication des différents termes
3 Utilisation de la formule
- 3.1 Équation de la vallée de la stabilité
4 Notes et références
5 Articles connexes

Expression

$B(A, Z)= a_vA - a_sA^\frac{2}{3} - a_c\frac{Z (Z-1)}{A^{\frac{1}{3}}} - a_a\frac{(A-2Z)^2}{A} \pm a_pA^{-\frac{1}{2}}$

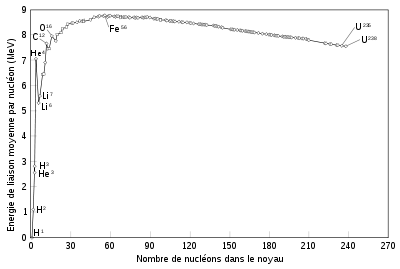Courbe représentant l'énergie de liaison par nucléon en fonction du nombre de nucléons dans le noyau.

où B est l'énergie de liaison, A est le nombre de masse (ou nombre de nucléons contenus dans le noyau A = Z+N), Z est le nombre de protons.

Les valeurs des constantes utilisées sont (en MeV) :

a_v = 15,56
a_s = 17,23
a_c = 0,7
a_a = 23,6
a_p = 11,2

Il existe différents jeux de paramètres pour la formule de Weizsäcker. Le choix du jeu de paramètres se définit en fonction des noyaux étudiés. Ainsi certains jeux de paramètres donneront des énergies de liaison plus précises pour les noyaux stables tandis que d'autres jeux donneront des résultats plus satisfaisant pour les noyaux exotiques.

Cette formule permet de retrouver les résultats expérimentaux ci-contre.

Explication des différents termes

La formule de Bethe-Weizsäcker fait apparaitre cinq termes :
$\,B=E_v+E_s+E_c+E_a+E_p$ .

Les deux premiers sont dus au modèle de la goutte liquide du noyau.
Le troisième exprime la répulsion électrostatique entre les protons.
Les deux dernières sont d'ordre quantique.

Pour expliquer ces différents termes, il faut supposer que le noyau est sphérique, de rayon $R 0$ . Et comme il est compact (son volume est proportionnel au nombre de nucléons A), alors $R 0$ est proportionnel à $A 1 / 3$ .

Énergie de volume

Pour expliquer le premier terme, on peut utiliser une analogie avec un gaz parfait pour lequel l'énergie interne est proportionnelle au nombre de particules constituant le gaz. Ainsi, on pose que cette énergie de volume $E v$ est proportionnelle à A. Elle permet d'expliquer les forces nucléaires de courtes portées, et la saturation des forces nucléaires :
$\,E_v = a_v A$ .

Énergie de surface

La notion de tension de surface sur une goutte liquide peut être utilisée pour interpréter le second terme. En effet, les nucléons à la surface du noyau sont en contact avec moins de nucléons que ceux du centre. L'énergie de liaison en est donc diminuée. Ainsi on introduit l'énergie de surface $E s$ , proportionnelle à la surface du noyau :
$\,E_s = -a_s A^{2/3}$ .
Le fait que la surface du noyau soit liée au nombre de nucléons est logique. Couramment, on fait l'approximation suivante^[1] :
$\,r = r_0 A^{1/3}$

r : le rayon du noyau.
$\,r_0$ = 1,2 fm : le rayon d'un nucléon.
A : le nombre de masse du nucléide considéré.

La surface d'une sphère étant $\,S=4 \pi r^{2}$ , en remplaçant r par son approximation :
$\,S = 4 \pi (r_0 A^{1/3})^{2} = 4 \pi r_0^{2} A^{2/3} = C A^{2/3}$
Avec C une constante définie par : $\,C = 4 \pi r_0^{2}$ , donc le coefficient de surface $\,a_s$ dépend de -C.

Répulsion électrostatique

Les protons étant tous chargés positivement, il se repoussent mutuellement. Cela participe à diminuer l'énergie de liaison par un terme de répulsion électrostatique $E c$ . Dans une approximation grossière, le noyau peut être considéré comme une sphère avec une densité de charge uniforme. L'énergie potentielle d'une telle distribution de charge est donnée par :

$E = \frac{3}{5} \left( \frac{1}{4 \pi \epsilon_{0}} \right) \frac{Q^{2}}{R}$

où $Q$ est la charge totale, $R$ le rayon de la sphère. En identifiant $Q$ à $Z e$ et en prenant le rayon proportionnel à $A 1 / 3$ , on obtient la forme du terme coulombien. Cependant, la répulsion coulombienne n'existe que lorsqu'il y a plus d'un proton ce qui induit que $Z 2$ devient $Z (Z - 1)$ . La valeur de $a c$ peut être calculée approximativement en utilisant l'équation ci-dessus :

$R = r_0 A^{\frac{1}{3}}$

Q = Z e

Z 2 = Z (Z - 1)

$E_c = \frac{3}{5} \left( \frac{1}{4 \pi \epsilon_{0}} \right) \frac{Q^{2}}{R} = \frac{3}{5} \left( \frac{1}{4 \pi \epsilon_{0}} \right) \frac{(Ze)^{2}}{(r_0 A^{\frac{1}{3}})} = \frac{3 e^2 Z^2}{20 \pi \epsilon_{0} r_0 A^{\frac{1}{3}}} = \frac{3 e^2 Z(Z - 1)}{20 \pi \epsilon_{0} r_0 A^{\frac{1}{3}}} = a_{C} \frac{Z(Z-1)}{A^{1/3}}$

L'énergie potentielle de la distribution de charge est donc :

$E_c = \frac{3 e^2 Z(Z - 1)}{20 \pi \epsilon_{0} r_0 A^{\frac{1}{3}}}$

La constante $a c$ du terme de répulsion électrostatique est :

$a_{c} = \frac{3 e^2}{20 \pi \epsilon_{0} r_0}$

Une autre valeur de $a c$ peut être obtenue en utilisant la constante de structure fine :

$a_{C} = \frac{3}{5} \left( \frac{\hbar c \alpha}{r_0} \right)$

où $α$ est la constante de structure fine, $r 0 A 1 / 3$ , le rayon du noyau avec $r 0$ qui vaut approximativement 1,25 femtomètres. Cela donne une valeur théorique de $a c$ de 0,691 MeV ce qui est peu éloigné des valeurs mesurées.

a c = 0,691 M e V

Énergie d'asymétrie

La répulsion électrostatique étant en compétition avec l'interaction forte pour stabiliser le noyau, les noyaux lourds ont besoin d'un surplus de neutrons afin que cette interaction forte contrebalance l'effet de la répulsion électrostatique. Il y a donc une asymétrie du nombre de neutrons par rapport au nombre de protons. Cela n'a, a priori, aucun autre effet sur l'énergie de liaison que ceux qui ont été étudiés plus haut. En réalité, un effet quantique va jouer un rôle : les nucléons se trouvent sur des niveaux d'énergie, ce qui fait qu'un surplus de neutrons va augmenter leur énergie. On obtient alors que l'effet sur l'énergie de liaison s'écrit : $E_a=-a_a\frac{(N-Z)^2}{A}=-a_a\frac{(A-2Z)^2}{A}$ .

Énergie d'appariement

Un deuxième effet quantique joue un rôle dans l'énergie de liaison : les nucléons ayant un spin demi-entier ont tendance à s'apparier deux à deux, pour se grouper préférentiellement en nombre pair. Ainsi, un nombre impair de neutrons ou de protons sera moins stable.
Une formule empirique permet de rendre compte de cet effet en posant une énergie d'appariement (ou de parité) $E p$ ayant différentes valeurs selon qu'il y ait un nombre pair ou impair de neutrons ou de protons :
$E_p=a_p\left\{ \begin{matrix} +A^{-\frac{1}{2}} & \mbox{cas pair-pair}\;\;\;\;\;\;\;\; \\ 0 & \mbox{cas pair-impair}\;\;\;\; \\ -A^{-\frac{1}{2}} & \mbox{cas impair-impair} \end{matrix}\right.$

Utilisation de la formule

Équation de la vallée de la stabilité

Pour un nombre de masse donné A, on s'aperçoit que la formule de Bethe-Weizsäcker fournit une équation quadratique en fonction de la charge Z. On a ainsi :

$B_A(Z) = (-a_c A^{-\frac{1}{3}} - 4 a_a A^{-1})Z^2 + (a_c A^{-\frac{1}{3}} + 4 a_a) Z + (a_v - a_a) A - a_s A^{\frac{2}{3}} \pm a_p A^{-\frac{1}{2}}$

Par définition, les noyaux stables sont définis comme étant des noyaux qui minimisent l'énergie de liaison $B A (Z)$ . Ainsi en cherchant les valeurs de $Z$ qui annulent la dérivée $B A (Z)$ par rapport à $Z$ , on peut obtenir une équation donnant les noyaux de la vallée de stabilité.

$\frac{\partial B_A(Z)}{\partial Z} = 0 \rightarrow Z = \frac{a_c A^{-\frac{1}{3}} + 4 a_a}{2(a_c A^{-\frac{1}{3}} + 4 a_a A^{-1})} \approx {1\over 2} {A\over 1 + A^{2/3} \frac{a_c}{4 a_a}}$

Notes et références

↑ http://www.sciences-en-ligne.com/DIST/Data/Ressources/lic2/chimie/chi_gen/chimie_structurale/noyau_atomique.htm

Dictionnaires et Encyclopédies sur 'Academic'

Formule de Weizsäcker

Sommaire

Expression