- Fonction À Sens Unique
-
Fonction à sens unique
Une fonction à sens unique est une fonction qui peut être aisément calculée, mais difficile à inverser — c'est-à-dire qu'étant donnée une image, il est difficile de lui trouver un antécédent. Les fonctions à sens unique sont utilisées en cryptographie asymétrique et dans les fonctions de hachage cryptographiques.
Exemple
Soient deux nombres premiers
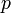 et
et 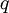 . Calculer
. Calculer 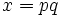 est facile même si
est facile même si 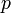 et
et 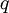 sont très grands. Par contre, on ne sait pas retrouver en pratique
sont très grands. Par contre, on ne sait pas retrouver en pratique 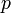 et
et 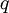 à partir de
à partir de 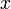 si
si 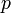 et
et 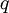 sont suffisamment grands. C'est le problème de la factorisation. On construit alors facilement à partir de x des fonctions dont le calcul de l'inverse ne serait possible qu'en connaissant p et q (voir RSA pour plus de détails), et qui sont donc (en pratique, tant que le problème de la factorisation n'est pas résolu) des fonctions à sens unique.
sont suffisamment grands. C'est le problème de la factorisation. On construit alors facilement à partir de x des fonctions dont le calcul de l'inverse ne serait possible qu'en connaissant p et q (voir RSA pour plus de détails), et qui sont donc (en pratique, tant que le problème de la factorisation n'est pas résolu) des fonctions à sens unique.Fonctions à brèche secrète
Certaines fonctions à sens unique sont appelées fonctions à brèche secrète en raison d'une « brèche secrète » qui permet à quelqu'un la connaissant de revenir facilement en arrière. Ce principe est utilisé entre autres pour le cryptosystème RSA, la clé privée (obtenue à partir des nombres p et q ci-dessus) étant la brèche.
De telles fonctions sont difficiles à trouver et tous les problèmes ne s'y prêtent pas. On pense que les fonctions basées sur le problème du logarithme discret (modulo un nombre premier ou défini sur le groupe d'une courbe elliptique) ne sont pas des fonctions à brèche secrète, car les groupes considérés ne semblent pas avoir de trappes connues[réf. nécessaire].
- Portail de la cryptologie
Catégorie : Cryptologie
Wikimedia Foundation. 2010.
