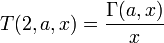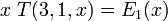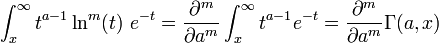- Fonction gamma incomplete
-
Fonction gamma incomplète
 Pour les articles homonymes, voir gamma (homonymie).
Pour les articles homonymes, voir gamma (homonymie).Définition
Il existe plusieurs définitions de fonction gamma incomplète (liste à compléter) :
Telles que définies dans Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, New York, 1964 (ISBN 0-486-61272-4)
Dérivées
La dérivée de la fonction gamma incomplète Γ(a,x) par rapport à x est bien connu. Elle est tout simplement fournie par la l'intégrande de sa définition intégrale:
La dérivée par rapport au paramètre a est fournie par[1]
et la deuxième dérivée est:
où la fonction "T(m,a,x)" est un cas spécial de la fonction de Meijer G
Ce cas particulier possède des propriétés internes de fermeture qui lui sont propres parce qu'il permet d'exprimer toutes les dérivées successives. En général,
où
Toutes ces dérivées peuvent être produites à partir de:
et
Cette fonction T(m,a,x) peut être calculée par sa représentation de série à condition que | z | < 1,
et pourvu que le paramètre a n'est pas un entier négatif ou zéro. Dans ce cas dernier, on doit employer une limite. Des résultats pour
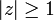 peuvent être obtenus par le prolongement analytique. Quelques cas spéciaux de cette fonction peuvent être simplifiés. Par exemple,
peuvent être obtenus par le prolongement analytique. Quelques cas spéciaux de cette fonction peuvent être simplifiés. Par exemple,où E1(x) est l'Exponentielle intégrale. Les dérivées et la fonction T(m,a,x) fournissent les solutions exactes à un certain nombre d'intégrales par la différentiation répétée de la définition intégrale de la fonction gamma incomplète Γ(a,x). Par exemple,
Cette formule peut être "gonflée" davantage ou généralisée à une classe considérable de transformées de Laplace ou de Mellin. Une fois combinée avec un système de calcul formel, l'exploitation des fonctions spéciales fournit une méthode puissante pour résoudre des intégrales définies, en particulier celles rencontrées par les applications pratiques des ingénieurs. Cette méthode fut inventée par les réalisateurs du système Maple[2] et alors plus tard émulée par Mathematica, MuPAD et d'autres systèmes. La fonction T(m,a,x) fut connue dans le groupe de recherche Maple comme la fonction de Scott-G.
Notes
- ↑ K.O Geddes, M.L. Glasser, R.A. Moore et T.C. Scott, Evaluation of Classes of Definite Integrals Involving Elementary Functions via Differentiation of Special Functions, AAECC (Applicable Algebra in Engineering, Communication and Computing), vol. 1, (1990), pp.149-165, [1]
- ↑ K.O. Geddes et T.C. Scott, Recipes for Classes of Definite Integrals Involving Exponentials and Logarithms, Proceedings of the 1989 Computers and Mathematics conference, (tenu à MIT June 12, 1989), édité par E. Kaltofen et S.M. Watt, Springer-Verlag, New York, (1989), pp. 192-201. [2]
- Portail des mathématiques
Catégories : Fonction gamma ou associée | Fonctions spéciales -
Wikimedia Foundation. 2010.

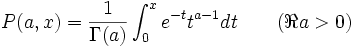
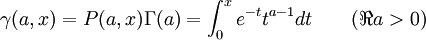
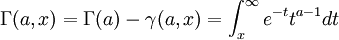
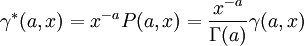
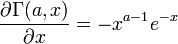
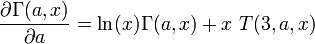
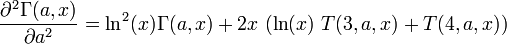
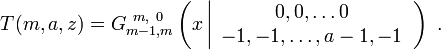

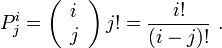
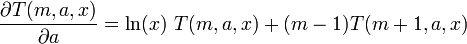
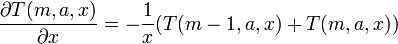
![T(m,a,z) = - \frac{(-1)^{m-1} }{(m-2)! } \frac{d^{m-2} }{dt^{m-2} } \left. (\Gamma (a-t) z^{t-1} ) \right]_{t=0} + \sum_{i=0}^{\infty} \frac{(-1)^i z^{a-1+i}}{i! (-a-i)^{m-1} }](/pictures/frwiki/53/542b397b00c838e7c7a7851be94ffdde.png)