Foncteur oubli
- Foncteur oubli
-
Foncteur
En mathématiques, le foncteur est la généralisation aux catégories de la notion de morphismes.
Définitions
Un foncteur 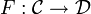 d'une catégorie
d'une catégorie  dans une catégorie
dans une catégorie 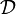 est la donnée
est la donnée
- d'une fonction qui, à tout objet A de
 , associe un objet F(A) de
, associe un objet F(A) de 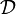 ,
,
- d'une fonction qui, à tout morphisme
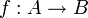 de
de  , associe un morphisme
, associe un morphisme 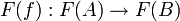 de
de 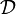 ,
,
qui
- respectent les identités: pour tout objet A de
 ,
,
- F(idA) = idF(A),
- respectent la composition: pour tous objets A, B et C et morphismes
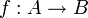 et
et 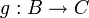 de
de  ,
,
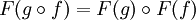 .
.
Un foncteur contravariant d'une catégorie  dans une catégorie
dans une catégorie 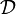 est un foncteur de
est un foncteur de 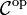 dans
dans 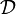 . Pour souligner le fait qu'il n'est pas contravariant un foncteur est parfois appelé foncteur covariant.
. Pour souligner le fait qu'il n'est pas contravariant un foncteur est parfois appelé foncteur covariant.
Foncteurs adjoints
Soient C et D deux catégories, F un foncteur de C dans D et G de D dans C tels que pour tout objet 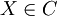 et
et 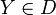 on ait une bijection naturelle en X et Y
on ait une bijection naturelle en X et Y 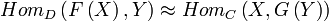 . Alors F et G sont des foncteurs adjoints, F est adjoint à gauche de G et G est adjoint à droite de F.
. Alors F et G sont des foncteurs adjoints, F est adjoint à gauche de G et G est adjoint à droite de F.
Exemples
- Le foncteur identité d'une catégorie
 , souvent noté
, souvent noté 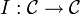 , qui laisse les objets et les morphismes de la catégorie invariants.
, qui laisse les objets et les morphismes de la catégorie invariants.
- Les foncteurs d'oubli qui envoient les objets d'une catégorie sur des objets d'une autre catégorie en « oubliant » certaines propriétés de ces objets :
-
- le foncteur de Ab dans Grp qui à un groupe abélien associe le groupe lui-même, mais dans la catégorie qui contient aussi les groupes non abéliens (on a « oublié » le fait que le groupe est abélien) ;
- le foncteur de Grp dans Set qui à un groupe associe l'ensemble sous-jacent (on a « oublié » la structure de groupe).
- Le foncteur de faisceaux, d'une catégorie dans la catégorie de ses faisceaux, qui associe à chaque objet X le faisceau
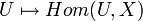 et son dual (contravariant) qui lui associe
et son dual (contravariant) qui lui associe 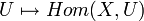 . Dans ce cas Hom( * ,pt) est le faisceau terminal (ou constant ou point) et
. Dans ce cas Hom( * ,pt) est le faisceau terminal (ou constant ou point) et 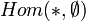 l'initial (ou vide). Le foncteur de faisceau est une représentation d'une catégorie dans son topos et permet d'identifier chaque objet au faisceau qu'il représente.
l'initial (ou vide). Le foncteur de faisceau est une représentation d'une catégorie dans son topos et permet d'identifier chaque objet au faisceau qu'il représente.
Propriété
L'image d'un isomorphisme par un foncteur est un isomorphisme.
Remarques
- Le foncteur constant (tous les objets ont le même objet image et chaque flèche est envoyée sur l'identité) est l'objet terminal de la catégorie des foncteurs).
- Les foncteurs sont parfois appelés morphismes pour la catégorie des catégories.
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie des catégories
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Foncteur oubli de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Foncteur adjoint — La notion d adjonction est fondamentale. Elle généralise la notion d équivalence entre deux catégories. En effet, si et définissent une équivalence de catégorie entre et , alors, F et G sont adjoints l un à l autre (et ce, « de tous les… … Wikipédia en Français
Foncteur — En mathématiques, le foncteur est la généralisation aux catégories de la notion de morphisme. Sommaire 1 Définitions 1.1 Foncteurs adjoints 2 Exemples 3 … Wikipédia en Français
Adjoint (foncteur) — La notion d adjonction est fondamentale. Elle généralise la notion d équivalence entre deux catégories. En effet, si et définissent une équivalence de catégorie entre et , alors, F et G sont ajoints l un à l autre (et ce, de tous les côtés… … Wikipédia en Français
Théorie des catégories — La théorie des catégories étudie les structures mathématiques et les relations qu elles entretiennent. Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l informatique théorique et en… … Wikipédia en Français
Algèbre universelle — Pour les articles homonymes, voir Algèbre (homonymie). L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces … Wikipédia en Français
CATÉGORIES ET FONCTEURS — Introduite en 1945 par Eilenberg et MacLane pour rendre compte de propriétés très générales des structures mathématiques, la théorie des catégories a quelque peu pâti, à ses débuts, de cette généralité qui lui valut auprès des «mathématiciens… … Encyclopédie Universelle
Algebre universelle — Algèbre universelle L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de… … Wikipédia en Français
Algèbre Universelle — L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de définir de manière… … Wikipédia en Français
Somme (catégorie) — Pour les articles homonymes, voir Somme. Dans une catégorie, la somme peut s exprimer par une propriété universelle ou de manière équivalente comme foncteur représentable. Sommaire 1 Définition 2 … Wikipédia en Français
Limite inductive — Sommaire 1 Avant propos 2 Ensemble ordonné filtrant 3 Système inductif 4 Propriété universelle de la limite inductive … Wikipédia en Français
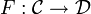 d'une catégorie
d'une catégorie  dans une catégorie
dans une catégorie 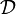 est la donnée
est la donnée , associe un objet F(A) de
, associe un objet F(A) de 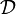 ,
,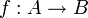 de
de  , associe un morphisme
, associe un morphisme 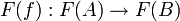 de
de  ,
, ,
,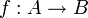 et
et 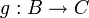 de
de  ,
,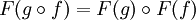 .
. dans une catégorie
dans une catégorie 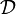 est un foncteur de
est un foncteur de 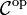 dans
dans 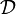 . Pour souligner le fait qu'il n'est pas contravariant un foncteur est parfois appelé foncteur covariant.
. Pour souligner le fait qu'il n'est pas contravariant un foncteur est parfois appelé foncteur covariant.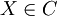 et
et 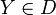 on ait une bijection naturelle en X et Y
on ait une bijection naturelle en X et Y 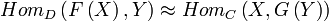 . Alors F et G sont des foncteurs adjoints, F est adjoint à gauche de G et G est adjoint à droite de F.Article détaillé : Adjoint (foncteur).
. Alors F et G sont des foncteurs adjoints, F est adjoint à gauche de G et G est adjoint à droite de F.Article détaillé : Adjoint (foncteur). , souvent noté
, souvent noté 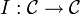 , qui laisse les objets et les morphismes de la catégorie invariants.
, qui laisse les objets et les morphismes de la catégorie invariants.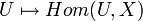 et son dual (contravariant) qui lui associe
et son dual (contravariant) qui lui associe 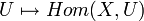 . Dans ce cas Hom( * ,pt) est le faisceau terminal (ou constant ou point) et
. Dans ce cas Hom( * ,pt) est le faisceau terminal (ou constant ou point) et 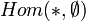 l'initial (ou vide). Le foncteur de faisceau est une représentation d'une catégorie dans son topos et permet d'identifier chaque objet au faisceau qu'il représente.
l'initial (ou vide). Le foncteur de faisceau est une représentation d'une catégorie dans son topos et permet d'identifier chaque objet au faisceau qu'il représente.