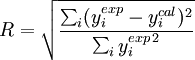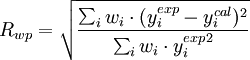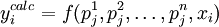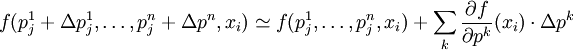Fitting

L'ajustement de courbe est une technique d'analyse d'une courbe expérimentale, consistant à construire une courbe à partir de fonctions mathématiques et d'ajuster les paramètres de ces fonctions pour se rapprocher de la courbe mesurée — on parle donc aussi d'ajustement de paramètres. On utilise souvent le terme anglais curve fitting ou simplement fitting, pour désigner cette méthode ; on utilise souvent le franglais « fitter une courbe » pour dire « ajuster une courbe ».

Dans les cas simples, on peut utiliser une méthode de régression : régression multilinéaire si la loi est linéaire pour tous les paramètres, interpolation polynomiale lorsque l'on utilise un polynôme pour simuler le phénomène (les paramètres physiques pouvant être déduits des coefficients du polynôme).

Les méthodes de régression permettent de déterminer les paramètres à partir de calculs sur les données, mais sont inapplicables si la fonction est trop complexe. Il faut alors travailler par essai-erreur pour se rapprocher d'une solution. La solution n'est pas nécessairement unique. C'est une méthode des moindres carrés.

Sommaire 1 Fonction utilisée 2 Démarche 3 Applications 4 Voir aussi 4.1 Articles connexes 4.2 Liens externes

Fonction utilisée

Dans certains cas, on a un modèle théorique permettant de prévoir la forme de la courbe ; la méthode d'ajustement permet de déterminer les paramètres de l'échantillon. Dans d'autres cas, on utilise une fonction empirique ; on s'intéresse alors en général à la surface, la largeur ou à la position du maximum de la fonction.

De manière générale, on a une fonction ƒ ayant n paramètres p¹, p², …, pⁿ qui relie l'abscisse x à l'ordonnée y :

y = ƒ(p₁, p², …, pⁿ, x)

et l'on compare cette fonction avec les m points expérimentaux

[(x₁, y₁^exp), (x₂, y₂^exp), …, (x_m, y_m^exp)]

La fonction ƒ peut être parfois décomposée en plusieurs fonctions ƒ₁, ƒ₂… soit qu'elle en est la somme, le produit, le produit de convolution…

ƒ = ƒ₁ + ƒ₂ +…

ou

ƒ = ƒ₁׃₂×…

ou

ƒ = ƒ₁*ƒ₂*…

Démarche

On calcule les points y_i^cal de la courbe simulée :

y_i^cal = ƒ(x_i)

Habituellement, on utilise un algorithme visant à minimiser l'écart quadratique entre la courbe simulée et la courbe expérimentale ; on parle d'algorithme de minimisation de l'erreur.

On définit donc un facteur de fiabilité (reliability factor) R :

où y_i^exp est le i-ème point mesuré et y_i^calc est le i-ème point calculé. R est similaire dans son expression au coefficient de corrélation multiple (R ² étant alors le coefficient de détermination). On utilise plus couramment le facteur de fiabilité pondérée (weighted reliability factor) R_wp :

où w_i est le poids attribué au point i ; ce poids représente l'incertitude associée au point i.

C'est donc un algorithme itératif : à chaque étape, on modifie un ou plusieurs facteurs et on regarde si cela provoque une diminution ou une augmentation de la fonction de fiabilité. Le jeu de paramètre retenu pour l'étape suivante est celui qui donne la plus faible valeur du facteur de fiabilité. Le calcul s'arrête lorsque l'on n'arrive plus à diminuer le facteur de fiabilité, on parle de convergence.

Si l'on note (p^k) l'ensemble des paramètres, l'intensité calculée en chaque point i à l'étape j s'exprime par

Pour simplifier les calculs, on peut faire un développement limité du premier ordre de cette fonction ƒ, alors en appliquant des petites perturbations Δp^k aux paramètres, on peut écrire

en imposant y_i^calc = y_i^exp, on obtient ainsi un ensemble d'équations linéaires qui peut se résoudre par une inversion de matrice, ce qui permet de calculer les Δp^k et donc les valeurs des paramètres à l'étape suivante j + 1. On peut aussi utiliser un algorithme plus complexe utilisant les dérivées secondes.

Il peut arriver que le programme converge vers un minimum local de R qui n'est pas le minimum absolu. Pour éviter cette situation, on utilise l'algorithme de Metropolis : lorsque l'on a convergé, on fait varier les paramètres d'une certaine valeur et on recommence le processus pour voir si l'on arrive à converger vers un autre jeu de paramètres ayant un facteur de fiabilité plus faible.

Si la simulation était parfaite, le facteur de fiabilité aurait une valeur dépendant du rapport signal sur bruit. Si l'on sait calculer ce rapport signal sur bruit, c'est-à-dire si l'on connaît la loi de probabilité régissant les fluctuations du signal, on peut alors déterminer un facteur de fiabilité incompressible R₀. Si la simulation est parfaite, on a alors

R = R₀

de fait, la qualité de la simulation est souvent exprimée par le rapport R/R₀, qui doit tendre vers 1 au fur et à mesure des étapes itératives.

Applications

• Déconvolution
• Méthode de Rietveld

Voir aussi

Articles connexes

• Approximation de fonction
• Interpolation (mathématiques)
• Régression multilinéaire

Liens externes

• Développement d'un programme d'ajustement de courbes, Département de Physique-EEA de l'Université de Caen Basse-Normandie