- Fermeture de kleene
-
Fermeture de Kleene
Pour les articles homonymes, voir Fermeture.La fermeture de Kleene, parfois appelée étoile de Kleene ou encore fermeture itérative, est un opérateur unaire utilisé pour décrire les langages formels. Appliquée à un ensemble V, elle a pour résultat le langage
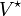, défini ainsi :- Si V est un alphabet, c'est-à-dire un ensemble fini de symboles ou caractères, alors 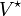est l'ensemble des mots sur V, mot vide ε inclus.
- Si V est un langage, alors 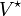est le plus petit langage qui le contienne, qui contienne {ε} et qui soit stable par concaténation (la concaténation de deux éléments de 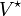est également dans ).
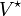Exemple d'application de l'étoile de Kleene à un alphabet :
- {'a', 'b', 'c'}* = {ε, « a », « b », « c », « aa », « ab », « ac », « ba », « bb », « bc », ...}
Exemple d'application de l'étoile de Kleene à un langage :
- {« ab », « c »}* = {ε, « ab », « c », « abab », « abc », « cab », « cc », « ababab », « ababc », « abcab », « abcc », « cabab », « cabc », « ccab », « ccc », ...}
L'étoile de Kleene est l'un des trois opérateurs de base utilisés pour définir une expression rationnelle, avec la concaténation et l'union ensembliste.
On généralise souvent l'étoile de Kleene à tout monoïde (M,.), où
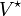, avec 
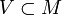, désigne la clôture de V par la loi « . », à laquelle on joint ε, l'élément neutre du monoïde. En d'autres termes 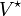est le plus petit ensemble contenant 
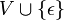, et stable par « . ». Il s'agit effectivement d'une généralisation, car l'ensemble des mots sur un alphabet est un monoïde dont la loi de composition interne est la concaténation, et l'élément neutre est le mot vide.Voir aussi
Portail des mathématiques
Portail de l’informatique
Portail de la logique
Catégories : Langage formel | Stephen Cole Kleene - Si V est un alphabet, c'est-à-dire un ensemble fini de symboles ou caractères, alors
Wikimedia Foundation. 2010.
